投机解码技术

参考文献：https://zhuanlan.zhihu.com/p/716344354

基本概念

LLM 模型属于自回归模型，主要包含两个阶段：Prefill 和 Decode 阶段。Prefill 阶段根据用户提供的 Prompt，批量处理 Prompt Tokens，生成第一个 Token 的输出，每个请求只执行一次 Prefill；而 Decode 阶段根据上一轮输出的 Token，作为当前轮次的输入，生成 Next Token，循环执行 Decode 直至生成终止符。通过实验可知，一个请求大部份生成 Token 时间都花在了 Decode 阶段，用户大部份时间都花在了等待 Decode 阶段完成。所以提升 Decode 阶段的生成 Token 效率可以很大程度提升用户的体验。

针对 Decode 阶段生成效率低的问题，越来越多的工作开始研究投机采样。投机采样的目的是将多步自回归解码合并成一步，仅通过一次 LLM 推理完成多个 Token 的生成。现有的投机采样的通用做法包含以下三个步骤：

1. 【初始阶段】原始 LLM 进行常规的自回归解码，采样第一个 Token；
2. 【Draft 阶段】使用一个尺寸较小的 Draft 模型，输入原始 LLM 生成的 Token，通过特定的采样方式生成连续若干个 Draft Tokens；
3. 【Verify 阶段】使用原始 LLM 验证 Draft Tokens 序列。

目前，Draft Tokens 的采样方式有两种，分别是 Token-Level 采样以及 Feature-Level 采样。

Token-Level 采样

在 LLM 生成任务中，有两个现象：

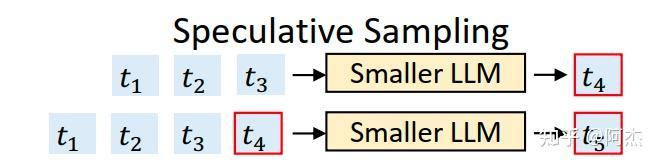
1. 在自回归任务中，生成 K 个 Token 需要迭代 K 步。其中不同的 Token 生成难度不同，有的 Token 更“容易” 生成，可以用更轻量、更高效的模型完成这类 Token 的生成；
2. LLM 在执行 Prefill 时，会并行生成 Token 序列对应的隐状态，对每个 Token 隐状态做一个 LM Head 的映射，可以得到每个 Token 对应的 Next Token 的概率。利用这个特性，可以将轻量模型生成出来的候选 Token 序列完成一次 LLM 的前向，得到候选 Token 序列对应的 Next Token 概率序列。通过该概率序列可以并行解码出若干个 Token，并且不会改变每个 Token 的生成概率分布。

利用这两个观察，作者提出 Speculative Decoding。Speculative Decoding 会选择一个比原始模型轻量的 LLM 作为 Draft 模型，在 Draft 阶段使用自回归采样的方式连续生成若干个候选 Token，如上图所示。在 Verify 阶段，将得到的候选 Token 序列放入到原始 LLM 做验证 & Next Token 生成，实现并行解码。每一轮 Draft Token 生成，输入都是上一轮采样后得到的 Draft Token，所以这种采样方式称为 Token-Level 采样。

• Speculative Decoding 存在的问题

在整个投机采样的流程中，假设轻量 LLM 生成 Draft Tokens 的开销为 $p$ ，原始 LLM 验证 & Next Token 生成的开销近似为 1，那么投机采样在接受 Tokens 数大于 $1+p$ 的情况下才有性能收益，并且随着接受的 Tokens 数增加而性能收益越大。所以投机采样要想获得性能收益，核心要解决以下两个问题：

1. 如何降低投机采样的 overhead?（即降低 $p$）
2. 如何提升 Verify 阶段的接受率？

为了解决这两个核心问题，选择一个合适的 Draft 模型就尤为重要。一般来说，越轻量的 Draft 模型，overhead 越低，但模型效果越差，导致接受率越低；越重的轻量模型，overhead 可能又过高，反而对性能造成伤害。针对这一个矛盾，Speculative Decoding 提供了一个性能表格，展示常用的原始模型在选择不同的 Draft 模型时，其 overhead、接受率以及最终的加速比情况。一般来说，在选择 Draft 模型时，选择一个同模型家族的轻量预训练模型，其 Token 生成的概率分布更接近，接受率更高。例如 LLaMA2 家族有 7B、13B 以及 70B 三种规格的预训练模型。原始模型为 70B 模型时，可以选择 7B 模型作为 Draft 模型。但是部署 13B 模型时，7B 模型就不是一个很好的选择，其 overhead 过大，很可能无法达到性能优化的目的。当遇到类似7B、13B模型时，很难找到一个更小的模型做 Draft 模型（也不一定能直接预训练一个更小的模型，除了训练成本较高以外，还因为无法获得与原始模型相同分布的预训练数据使得 Tokens 生成概率分布很难接近，导致接受率低）。

Feature-Level 采样

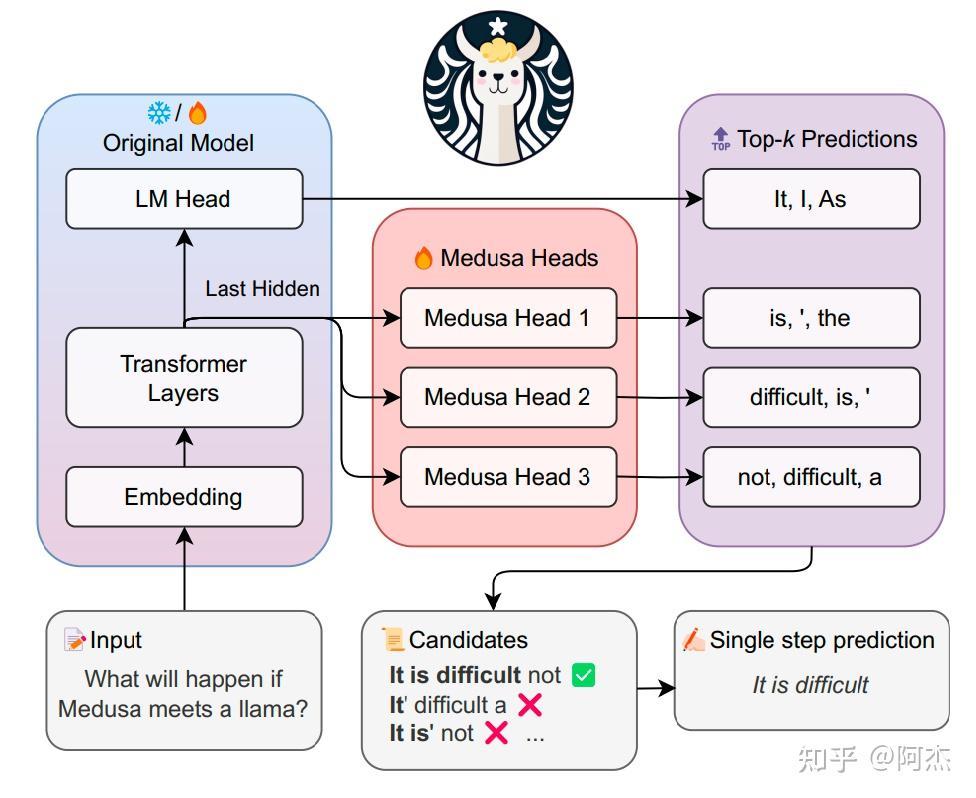
Speculative Decoding 难以获取 Draft 模型最核心的原因是 Draft 模型是一个独立的模型。独立模型意味着在训练 Draft 模型前要先挑选合适的轻量模型，并且必须满足训练成本低的特性，以达到和原始模型输出概率分布相近的收敛效果。这一步涉及大量的实验成本，也是其难以落地的重要原因。所以，独立的 Draft 模型是落地难的主要原因。针对 “独立” 这一特性，其中一个优化寻找 Draft 模型的思路是，通过复用原始 LLM 已有的权重，训练出参数规模较小的增量权重，这些增量的权重可以视作原始 LLM 的偏差，用于预测 Draft Token。这样可以保证生成 Token 时会先走原始 LLM 模型，然后通过叠加训练后的偏差，生成不同的 Draft Token。这种在生成 Draft Token 时复用原始 LLM 权重的方式也叫 Self Drafting。根据这个思路，Medusa 应运而生。

首先介绍 Medusa 如何生成 Draft Token。Medusa 通过插件的方式，在原始 LLM 模型基础上插入若干个 Medusa Head，通过 Medusa Head 生成不同的 Draft Tokens。其整体架构如上图所示。图中最左侧方框表示原始的 LLM 模型。左下角输入自然语言 Prompt，经过原始 LLM 模型计算，得到一个 Last Hidden（下称隐状态）。这个隐状态是原始 Prompt 的深层特征。这个深层特征具备很强的表达能力，通过这个深层特征可以很容易采样出 Next Token。在 Medusa 架构中，隐状态后会接入 LM Head（这个与常规的 LLM 一样） 以及若干个 Medusa Heads。LM Head 负责预测 Next Token，Medusa Heads 是 Medusa 架构中的增量权重，负责在 Draft 阶段预测 Draft Tokens。在多个 Medusa Head 中，Medusa Head 1 负责预测 Next Next Token，Medusa Head 2 负责预测 Next Next Next Token 等。每个 Medusa Heads的输入是原始 LLM 模型的隐状态输出而非 Token Embedding，所以 Medusa 采样属于 Feature-Level 采样。

在完成 Draft Token 生成后，需要验证 Draft Token。在介绍 Medusa 验证方式之前，我们先分析下 Draft Tokens 组成的路径数，即待验证的 Draft Tokens 序列的个数。Medusa 在 Draft 阶段通过一次前向批量生成若干个步的 Draft Tokens，每一步也对应若干个候选 Draft Tokens。假设 Medusa Heads 个数为 $N$，即每次 Draft 阶段会同时生成 $N$ 步；Medusa Head 下标为 $i$，对应生成第 $i$ 步的 Draft Tokens，每一步的 Draft Tokens 数量为 $C_i$，那么总的候选路径数则有 $\sum_{i=1}^{N}\prod_{j=1}^{i} C_i$ 个。

所以每次 Draft 阶段后，需要验证 $\sum_{i=1}^{N}\prod_{j=1}^{i} C_i$ 条路径，然后选匹配到最长的路径作为最终的输出。最笨的验证方法是串行验证每条路径，然后输出最长匹配的路径。但是这样需要反复调用原始 LLM 推理，其调用次数为 $\sum_{i=1}^{N}\prod_{j=1}^{i} C_i$，最多接收 $N$ 个 token。对比接收 $N$ 个 Token 仅需调用 $N$ 次原始 LLM 推理的自回归采样，性能会大幅下降。这决定了 Medusa 不能使用串行的方式验证所有路径，必须使用并行方式同时验证所有路径。为此 Medusa 提出 Tree Attention：

Tree-Attention

将所有路径拍平为一维的序列，将这个序列作为一个序列输入放到模型中运行。其中 Attention 阶段 Token 之间会进行注意力计算，为了避免不同路径之间的 Token 计算注意力，需要将其他 Token 加上 Mask，不让某一路径的 Token “看到” 其他路径的 Token。不同 Step 的 Draft Token 构造的路径形成一课树，即 Draft 树。不同 Step 的 Draft Token 在树中不同层的节点，所以上述的 Mask 也称为 Tree Mask。这个 Tree Mask 设计仿照 Casual Mask 的设计，为 Token 掩盖不应 “看到” 的其他 Token。

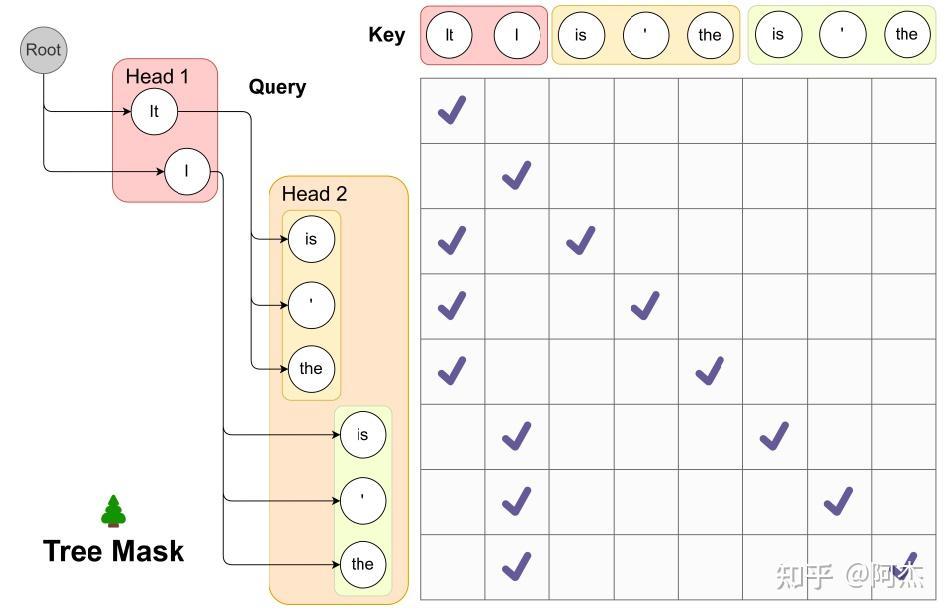
上图展示 Tree Attention 的过程。图中有两个 Medusa Heads，Medusa Head 1 生成 2 个 Draft Tokens，分别为 “It” 和 “I”；Medusa Head 2 生成 3 个 Draft Tokens，分别为 “is”、“'” 和 “the”。第一步需要构造验证序列。以 Medusa Head 1 的 Draft Token 为终点的路径一共有 2 条，这是树的第一层；以 Medusa Head 2 的 Draft Token 为终点的路径一共有 6 条，这是树的第二层。将所有路径糅合在一起，得到一个序列长度为 8 的验证序列。前两个 Token 为树第一层的两个节点，对应两条长度为 1 的路径。这两个 Token 只看到自己，所以上图矩阵中(0, 0)节点到(1, 1)节点的小矩阵的对角线上的 Mask 设置为 1；第 3 到第 5 个 Token，只看到自己以及前置的 Token “It”，所以在自己及 “It” 位置上的 Mask 值设置为 1；第 6 到第 8 个 Token 同理。再完成 Tree Mask 构造后，就可以通过 Tree Attention 完成一次原始 LLM 推理调用，批量验证所有 Draft 路径。

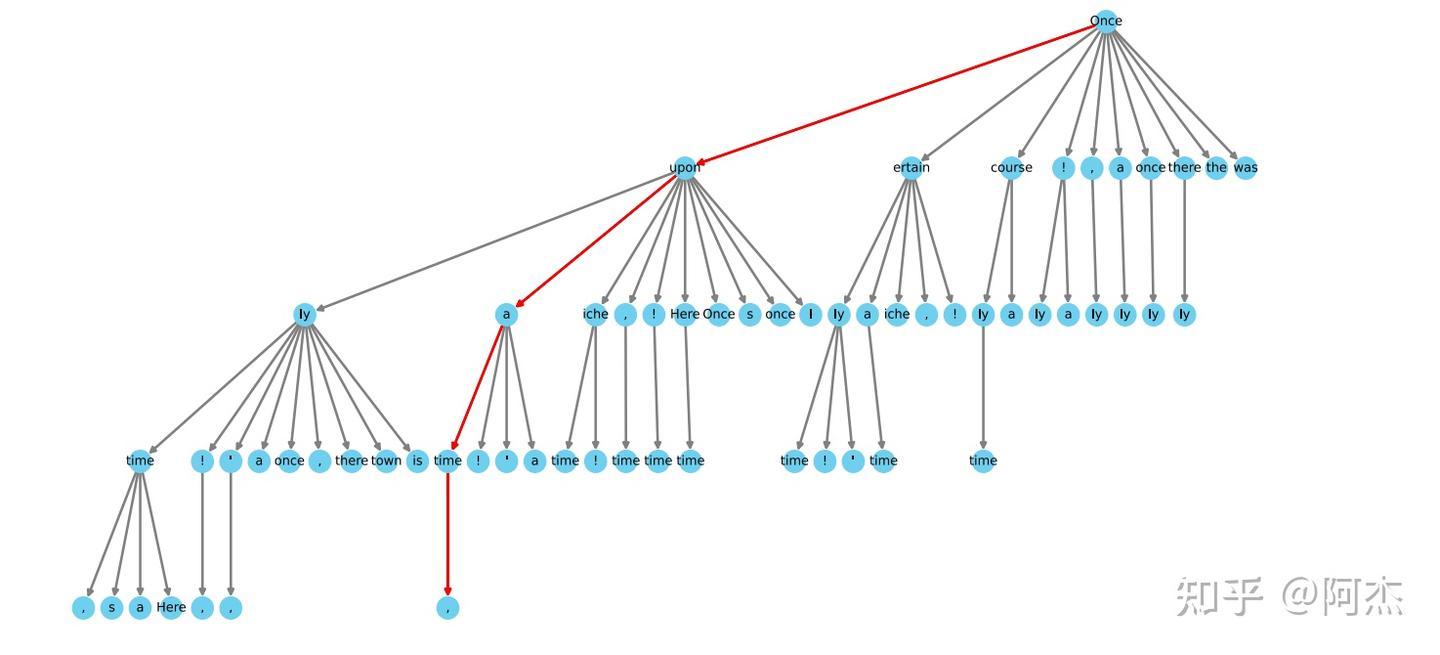
上述提到，Medusa 生成的 Draft Token 构造的路径数为 $\sum_{i=1}^{N}\prod_{j=1}^{i} C_i$，所以对应的验证序列的长度也为 $\sum_{i=1}^{N}\prod_{j=1}^{i} C_i$。为了保证接收率，$C_i$ 的设置不宜过小，作者提供的配置是 [10, 10, 9, 4]，对应的 Medusa Head 为 1 至 4。通过这个配置，可以得出构造的路径总数为 4610，对应的验证序列长度为 4610。这个长度在验证时会引入很大的 overhead。其实有大部份的路径接收概率很低，没必要验证，所以 Medusa 针对验证序列长度做了优化，通过先验的方式对 Draft 树 进行剪枝，将接收概率低的路径提前剪掉，缩短验证序列长度，避免浪费算力验证低概率路径。如下图是 Medusa 提供的一个剪枝后的 Draft 树，5 层共计 64 个节点，对应验证序列的长度为 64。

与 Speculative Decoding 相比，Medusa 有两大优势：

1. Draft 模型易于获取。Medusa 属于 Self Drafting 投机采样，仅需添加几个 Medusa Head 层，通过 SFT 即可获得 Medusa 模型。Medusa 根据训练资源提供了两种训练方式：Medusa 1 和 Medusa 2。Medusa 1 冻结主干的参数，仅训练 Medusa Head，所需的 GPU 数量及训练时间都很小（Vicuna 7B 仅需单卡 A100，5个小时的训练时间）；Medusa 2 联合主干模型进行微调，预测精度更高，所需的训练资源对比 Medusa 1 也更高一点。
2. 接收率更大。多个 Medusa Heads 并行采样，得到多条 Draft 路径。通过 Tree Attention 方式并行验证多个路径，提高单次投机采样的接收长度。除此之外，Draft Token 是通过隐状态采样得到的，理论上准确率会更高一些（Medusa 没有做消融实验，后面介绍的 EAGLE 有做相关的实验论证）。

Medusa 存在的问题

虽然 Medusa 对比 Speculative Decoding 有了很大的性能提升，但是仍然存在一些优化空间，主要包括两个方面：

1. 接收率。Medusa 主要因为采样过程以及笛卡尔积构造 Draft 路径造成的。Medusa 采用了隐状态并行预测多步 Draft Tokens，在预测间隔 Tokens 时（即 Next Token 以后的 Draft Token），Draft Token 并不知道上一个 Token 是什么，预测时不确定性增加，也影响了间隔 Tokens 的准确率。
2. Verify 效率。Medusa 利用 Decode 阶段算力利用率低的特点，用算力换时间。通过增大单次推理的计算规模，提高计算仿存比，降低总的推理次数，从而降低 Decode 的总时间。但是由于算力资源有限，单次推理的计算规模不能一直增大。LLM 的自回归采样阶段的计算规模会随着 batch size 增大而增大，其计算仿存比也会增大，直至 Compute Bound 的边界。这个边界对应着一个临界的 batch size。Medusa 单次推理验证 64 条路径，最多接收 4 个 Token，算力需求对比常规的自回归采样增大了 16 倍，计算仿存比也增长了 16 倍，到达 Compute Bound 临界点的 batch size 对比常规的自回归采样也大大缩小了。当 batch size 超越临界点后，算力资源不足，性能上对比自回归采样会下降，这一问题 Medusa 也在论文中提到。所以 Medusa 在大流量请求下性能可能会劣化，个人认为比较适合小流量场景。

小结

无论是 Speculative Decoding，还是 Medusa，都是围绕以下两个方面进行优化：

1. Draft Token 的接收率。这个主要依赖模型架构、算法设计以及模型训练。
2. 投机采样的 overhead。overhead 主要来源于 Draft Token 生成，采样后处理以及验证 Draft Token 的效率。

这两点直接影响投机采样的性能，也是各个投机采样的优化方向，EAGLE 也将从这两个方向进行算法优化。

EAGLE-1

2个重要观察

通过上文关于 Speculative Decoding 和 Medusa 的介绍，EAGLE的作者观察到两个现象：

1. Token-Level 自回归解码方式的不足：在自回归生成中，使用 Token 的隐藏层特征（Feature Level）比直接使用 Token Embedding 预测 Next Token 效果更好。这是因为 Token Embedding只是文本的一个简单转化，没有经过深层网络抽取特征，表达能力不足，在使用轻量 Draft 模型时预测效果会有折损；而 Token 的隐藏层特征指最后一层 TransformerLayer 的输出，LM Head 的输入。隐藏层特征经过深层网络的计算，其表达能力要强于 Token Embedding，也更适用于采样。常规的投机推理就是 Token Level 自回归解码方式，接收率受限；

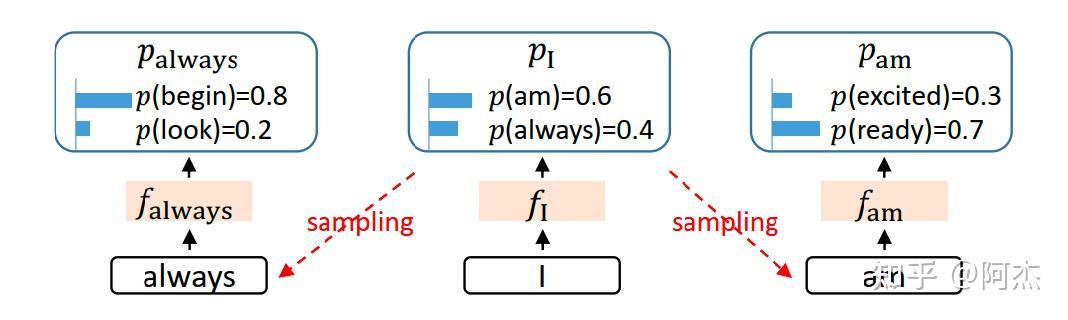
2. 采样算法的不确定性会限制生成 Next Token 的隐藏层特征的效果：当前 Token 的隐藏层特征经过 LM Head 后使用采样算法随机生成 Next Token。而在 Next Token 生成 Next Next Token 过程中，需要生成 Next Token 的隐藏层特征，该特征完全由 Next Token 决定，间接由采样算法决定。 采样算法具有随机性，有一定概率选择不同的 Next Token，这样使得 Next Token 的隐藏层特征也具有随机性，会影响 Next Next Token 的生成效果。如下图所示。当前 Token 为 “I”，对应的隐藏层特征为 $f_I$，可能会采样 “am” 和 “always”。这两个 Token 会通过模型计算得到隐藏层特征 $f_{am}$ 和 $f_{always}$。这两个隐藏层特征仅仅依赖 “am” 和 “always” 两个 Token 的Embedding 特征，与 $f_I$ 无关，所以隐藏层特征的生成非常依赖采样算法的结果，生成效果的稳定性不足，影响接收率。Medusa 也有类似的随机问题。虽然 Medusa 采样时使用隐藏层特征，但是在生成每一个 Draft Token 时，都缺乏上一个 Token 的信息，导致生成效果也不稳定。所以为了提高 Token 生成的稳定性，在生成当前 Token的隐藏层特征时，可以融合当前 Token 的 Embedding 以及上一个 Token 的隐藏层特征，保证 Draft Token生成时具备足够的信息，增强 Token 生成效果。

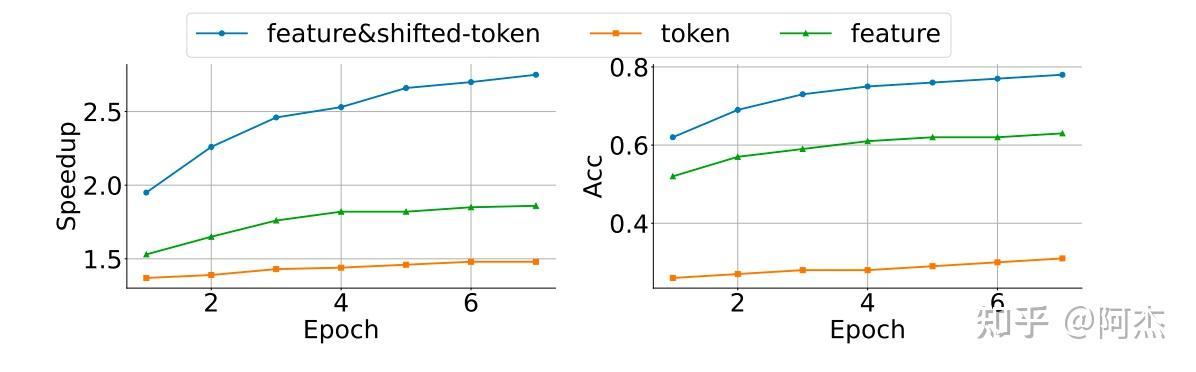
作者做了一个实验，比较了 Token-Level 以及 Feature-Level 采样算法的接收率与加速比。如下图所示。橙色曲线表示 Token-Level 采样算法，其接收率和加速比均是最低；绿色曲线表示 Feature-Level 采样算法，其接收率和加速比均比 Token-Level 采样算法要高；蓝色线表示 Feature-Level 和 Token-Level 的融合采样算法，模型的输入由当前 Token 的 Embedding 以及上一个 Token 的隐状态组成，该算法接收率和加速比均是最高，也是 EAGLE 将使用的加速算法。

方法

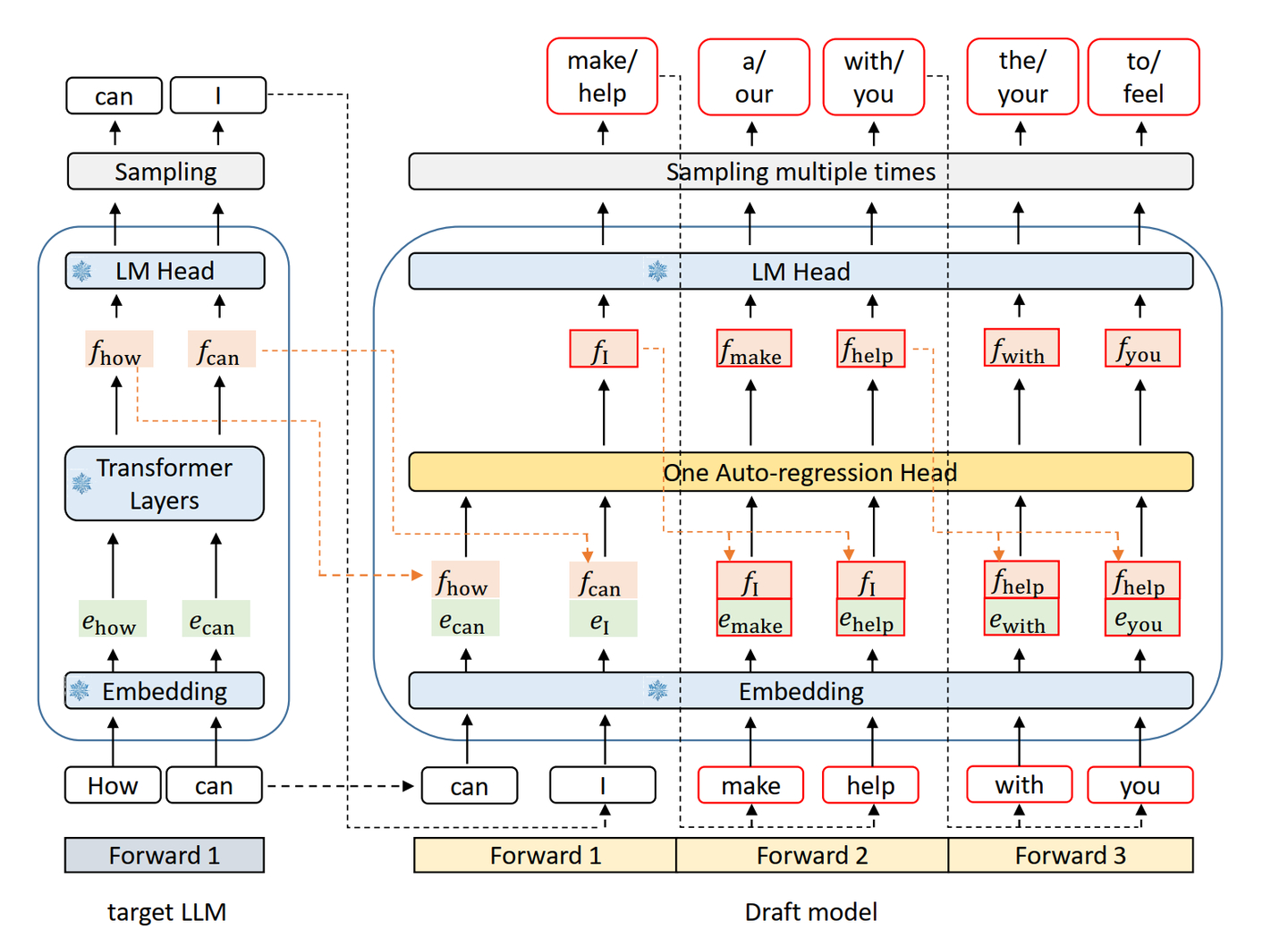
EAGLE 是一种投机采样方法，整体模型架构如下。左边是原始 LLM 模型，右边是 Draft 模型及其生成 Draft Token 的流程。Draft 模型是一个同构的轻量 LLM，其中 Embedding 层和 LM Head 层均复用原始 LLM 模型，中间的 One Auto-regression Head(简称 AR Head) 为由一层 FC 层以及一层 Transformer Layer 组成。AR Head 是唯一需要微调的网络层，训练成本也是极低。EAGLE 使用 Draft 模型通过自回归采样方式生成 Draft Tokens，并且为了提升接收率，在运行 AR Head 前会融合上一个 Token 的隐状态与当前 Token 的 Embedding层，并通过 AR Head 的 FC 层融合（形状从 [seq_len, hidden_size * 2] 变为 [seq_len, hidden_size]。在 Draft 阶段，自回归采样的第一轮输入是原始 LLM 模型生成的 Token，通过 TopK 采样生成第一轮的 Top $K_1$个 Draft Token。该 $K_1$个 Draft Token 作为第二轮输入，对应生成 $K_1$ 组Draft Tokens，每组通过采样生成 $K_2$ 个 Draft Token。下一轮会从当前轮中选择若干个 Draft Token 的输出作为输入，继续自回归采样，直至到达预设的运行轮次。

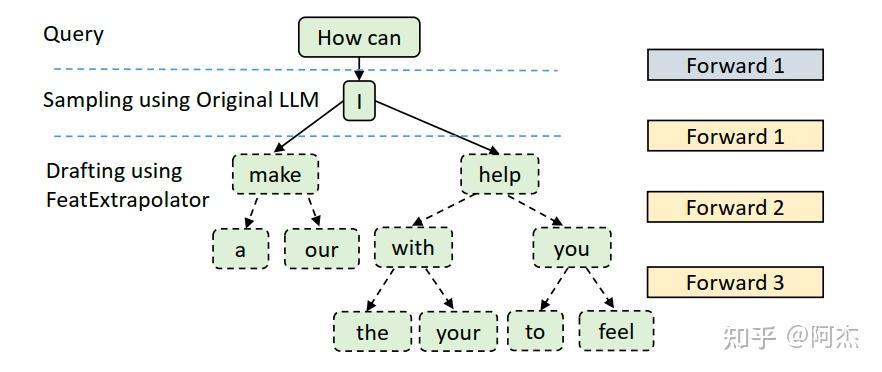
通过上述方式的 Draft 采样过程，就得到一颗 Draft 树， 如下图所示。 与 Medusa 不同的是，Draft 树并不是不同轮次的 Draft Tokens 通过笛卡尔积方式生成的，而是根据不同的 Draft Token，生成不同的Draft Token 子节点。这样的好处是：天然地去掉 Draft 树中无用的分支，使 Verify 阶段的验证序列长度大大缩小；使路径中每个节点之间的相关性更高，进一步提高接收率。

在生成 Draft 树后，Verify 阶段使用 Medusa 的 Tree Attention 进行验证，批量验证所有 Draft 路径。与 Medusa 类似，EAGLE 也使用先验的方式，提供一个静态的 Draft 树，如下图所示。对于任意输入，Draft 阶段都将按照图中所示的 Draft 树生成 Draft Tokens。