yitao's Blog
yitao's Blog

《面试经典150题》

yitao 收录于 找工作
 约 10100 字 预计阅读 20 分钟 

《面试经典150题》做题记录，原题单链接

数组/字符串

88.合并两个有序数组

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。 请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。 注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

腾讯PCG-青云 一、二面手撕
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        int p1 = m - 1, p2 = n - 1, p = m + n - 1;
        while (p2 >= 0) {
            if (p1 >= 0 && nums1[p1] > nums2[p2]) {
                nums1[p -- ] = nums1[p1 -- ];
            } else {
                nums1[p -- ] = nums2[p2 -- ];
            }
        }
    }
};

27.移除元素

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。 假设 nums 中不等于 val 的元素数量为 k，要通过此题，您需要执行以下操作： 更改 nums 数组，使 nums 的前 k 个元素包含不等于 val 的元素。nums 的其余元素和 nums 的大小并不重要。 返回 k。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

// 用栈存储去除后的元素
class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int top = 0;
        for (int x : nums) {
            if (x != val) {
                nums[top ++ ] = x;
            }
        }
        return top;
    }
};

26.删除有序数组中的重复项

给你一个 非严格递增排列 的数组 nums ，请你 原地 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。 考虑 nums 的唯一元素的数量为 k ，你需要做以下事情确保你的题解可以被通过： 更改数组 nums ，使 nums 的前 k 个元素包含唯一元素，并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。 返回 k 。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int siz = nums.size();
        int top = 0;

        for (int i = 0; i < siz; i ++ ) {
            int x = nums[i];
            if (i && x == nums[i - 1]) continue; // 跳过重复数字
            nums[top ++ ] = x;
        }
        return top;
    }
};

80.删除有序数组中的重复项 II

给你一个有序数组 nums ，请你 原地 删除重复出现的元素，使得出现次数超过两次的元素只出现两次 ，返回删除后数组的新长度。 不要使用额外的数组空间，你必须在 原地 修改输入数组 并在使用 $O(1)$ 额外空间的条件下完成。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

// 用栈模拟, top表示栈顶, 栈存储全部不重复元素
class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int top = 2;
        int siz = nums.size();

        for (int i = 2; i < siz; i ++ ) {
            if (nums[i] != nums[top - 2]) nums[top ++ ] = nums[i];
        }
        return min(top, siz);
    }
};

169.多数元素

给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数 大于 `⌊ n/2 ⌋`` 的元素。 你可以假设数组是非空的，并且给定的数组总是存在多数元素。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

// 摩尔投票法
class Solution {
public:
    int majorityElement(vector<int>& nums) {    
        int x = 0, votes = 0;
        for (int num: nums) {
            if (votes == 0) x = num;
            votes += num == x ? 1 : -1;
        }
        return x;
    }
};

189.轮转数组

给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]

示例 2:
输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        // 根据 k 计算出每个元素轮转后的位置，然后填入新的 vector 中
        int n = nums.size();
        k %= n;

        std::reverse(nums.begin(), nums.end());
        std::reverse(nums.begin(), nums.begin() + k);
        std::reverse(nums.begin() + k, nums.end());
    }
};

121.买卖股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

状态机模型
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        // 买入->卖出，求区间端点差值的最大值
        int ans = 0;
        int min_price = prices[0];
        for (int p : prices) {
            ans = max(ans, p - min_price);
            min_price = min(min_price, p);
        }
        return ans;
    }
};

122.买卖股票的最佳时机II

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。
在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。
返回 你能获得的 最大 利润 。

状态划分参考
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        // 状态机模型  
        // f[i][j]表示所有考虑前 i 个步骤，且第 i 个状态是 j(0未持股, 1持股)的集合，属性是最大值
        // 对于f[i][j]
        // 如果i-1步是0，0->0（未持股且不买入）；0->1（未持股且买入）；
        // 如果i-1步是1，1->0（持股且卖出）；1->1（持股且不卖出）        

        int n = prices.size();
        int INF = 0x3f3f3f3f;

        vector<vector<int>> f(n + 1, vector<int>(2, 0));  // f[n][2]
        prices.insert(prices.begin(), 0);

        f[0][0] = 0, f[0][1] = -INF;
        for (int i = 1; i <= n; i ++ ) {
            f[i][0] = max(f[i - 1][0], f[i - 1][1] + prices[i]);
            f[i][1] = max(f[i - 1][1], f[i - 1][0] - prices[i]);
        }

        return max(f[n][0], f[n][1]);
    }
};

55.跳跃游戏

给你一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false 。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Solution {
public:
    bool canJump(vector<int>& nums) {
        // 只要跳到了不为 0 的格子上，就一直可以往后跳
        // 转为合并区间问题
        int mx = 0;
        for (int i = 0; i < nums.size(); i ++ ) {
            if (i > mx) return false;
            mx = max(mx, i + nums[i]);
        }
        return true;
    }
};

45.跳跃游戏II

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向后跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

  • 0 <= j <= nums[i]
  • i + j < n
    返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

class Solution {
public:
    int jump(vector<int>& nums) {
        int ans = 0;
        int cur_right = 0; // 已建造的桥的右端点
        int next_right = 0; // 下一座桥的右端点的最大值

        for (int i = 0; i + 1 < nums.size(); i ++ ) {
            // 遍历的过程中，记录下一座桥的最远点
            next_right = max(next_right, i + nums[i]);
            if (i == cur_right) {  // 无路可走，必须建桥
                cur_right = next_right;  // 建桥后，最远可以到达 next_right
                ans ++ ;
            }
        }
        return ans;
    }
};

274.H指数

给你一个整数数组 citations ，其中 citations[i] 表示研究者的第 i 篇论文被引用的次数。计算并返回该研究者的 h 指数。 根据维基百科上 h 指数的定义：h 代表“高引用次数” ，一名科研人员的 h 指数 是指他（她）至少发表了 h 篇论文，并且 至少 有 h 篇论文被引用次数大于等于 h 。如果 h 有多种可能的值，h 指数 是其中最大的那个。

即：给你一个数组，求一个最大的 $h$，使得数组中有至少 $h$ 个数都大于等于 $h$。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution {
public:

    int hIndex(vector<int>& citations) {
        int n = citations.size();

        auto check = [&](int mid) -> bool {
            int n = citations.size();

            int res = 0;
            for (int i = 0; i < n; i ++ ) {
                if (citations[i] < mid) res ++ ;
            }
            return (n - res) >= mid;
        };

        int l = -1, r = n + 1;
        while (l + 1 < r) {
            int mid = l + (r - l) / 2;
            if (check(mid)) l = mid;
            else r = mid;
        }
        return l;
    }
};

380. O(1) 时间插入、删除和获取随机元素

实现RandomizedSet 类：

  • RandomizedSet() 初始化 RandomizedSet 对象
  • bool insert(int val) 当元素 val 不存在时，向集合中插入该项，并返回 true ；否则，返回 false 。
  • bool remove(int val) 当元素 val 存在时，从集合中移除该项，并返回 true ；否则，返回 false 。
  • int getRandom() 随机返回现有集合中的一项（测试用例保证调用此方法时集合中至少存在一个元素）。每个元素应该有 相同的概率 被返回。 你必须实现类的所有函数，并满足每个函数的 平均 时间复杂度为 O(1) 。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

// 哈希表 + 变长数组
class RandomizedSet {
public:
    RandomizedSet() {
        srand((unsigned)time(NULL));
    }

    bool insert(int val) {
        if (indices.count(val)) {
            return false;
        }
        int index = nums.size();
        nums.emplace_back(val);
        indices[val] = index;
        return true;
    }

   // 主要是这里，删除默认让尾部的值覆盖要删除的元素，然后erase掉指定的值
    bool remove(int val) {
        if (!indices.count(val)) return false;
        int index = indices[val];
        int last = nums.back();
        nums[index] = last;
        indices[last] = index;
        nums.pop_back();
        indices.erase(val);
        return true;
    }

    int getRandom() {
        int randomIndex = rand() % nums.size();
        return nums[randomIndex];
    }
private:
    vector<int> nums;
    unordered_map<int, int> indices;
};

/**
 * Your RandomizedSet object will be instantiated and called as such:
 * RandomizedSet* obj = new RandomizedSet();
 * bool param_1 = obj->insert(val);
 * bool param_2 = obj->remove(val);
 * int param_3 = obj->getRandom();
 */

238.除自身以外数组的乘积

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。题目数据 保证 数组 nums 之中任意元素的全部前缀元素和后缀的乘积都在 32位 整数范围内。请不要使用除法，且在 O(n) 时间复杂度内完成此题。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {

        // 用“前缀数组”和“后缀数组”完成
        int n = nums.size();
        vector<int> pre(n + 1, 1);
        vector<int> suf(n + 1, 1);

        vector<int> ans(n);

        for (int i = 1; i <= n; i ++ ) {
            pre[i] = pre[i - 1] * nums[i - 1];
        }

        for (int i = n - 1; i >= 1; i -- ) {
            suf[i] = suf[i + 1] * nums[i];
        }

        for (int i = 0; i < n; i ++ ) {
            ans[i] = pre[i] * suf[i + 1];
        }
        return ans;
    }
};

134.加油站

在一条环路上有 n 个加油站，其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。
给定两个整数数组 gas 和 cost ，如果你可以按顺序绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1 。如果存在解，则 保证 它是 唯一 的。

本题是特殊做法，通用做法是单调队列，详情见：AcWing.1088
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int n = gas.size();

        for (int i = 0, j = 0; i < n;) {  // 枚举起点
            int left = 0;
            for (j = 0; j < n; j ++ ) {  // 枚举走了几步
                int k = (i + j) % n;
                left += gas[k] - cost[k];
                if (left < 0) break;  // 如果剩余油量不够，则退出枚举，这里有个贪心思想，i~j 之间不用枚举
            }
            if (j == n) return i;
            i = i + j + 1;
        }
        return -1;
    }
};

135.分发糖果

n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。
你需要按照以下要求，给这些孩子分发糖果：

  • 每个孩子至少分配到 1 个糖果。
  • 相邻两个孩子中，评分更高的那个会获得更多的糖果。 请你给每个孩子分发糖果，计算并返回需要准备的 最少糖果数目 。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class Solution {
public:
    int candy(vector<int>& ratings) {
        int n = ratings.size();
        int ans = n;  // 每个孩子至少1个糖果
        for (int i = 0; i < n; i ++ ) {
            // 找起始点，满足递增才可以作为起始点
            int start = i > 0 && ratings[i - 1] < ratings[i] ? i - 1 : i;

            // 找严格递增段
            while (i + 1 < n && ratings[i] < ratings[i + 1]) {
                i ++ ;
            }
            // 循环结束时，i 为峰顶
            int top = i;

            // 找严格递减段
            while (i + 1 < n && ratings[i] > ratings[i + 1]) {
                i ++ ;
            }
            // 循环结束时，i 为谷底
            int inc = top - start;  // start 到 top 严格递增
            int dec = i - top;  // top 到 i 严格递减

            ans += (inc * (inc - 1) + dec * (dec - 1)) / 2 + max(inc, dec);  // 等差数列公式，由于求最少糖果数，所以公差为1
        }
        return ans;
    }
};

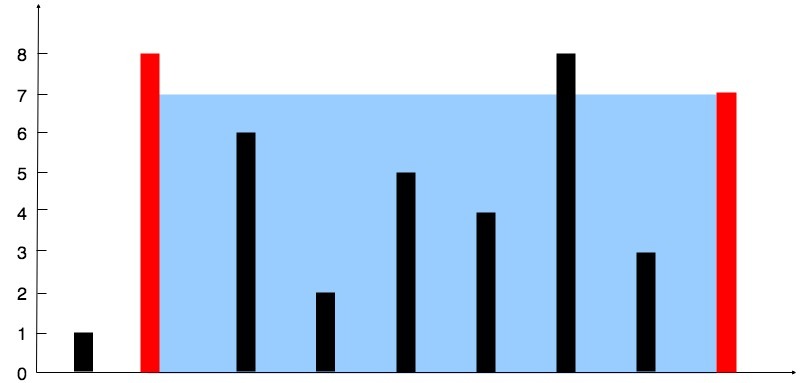
42.接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

123

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Solution {
public:
    int trap(vector<int>& height) {
        int n = height.size(), pre_max = 0, suf_max = 0;  // pre_max之前最高的柱子高度，suf_max之后最高的柱子高度

        // 注意到下标 i 处能接的雨水量由 pre_max[i] 和 suf_max[i] 中的最小值决定。
        int left = 0, right = n - 1, res = 0;
        while (left < right) {
            pre_max = max(pre_max, height[left]);   // 维护pre_max
            suf_max = max(suf_max, height[right]);  // 维护suf_max

            if (pre_max < suf_max) {
                res += pre_max - height[left];
                left ++ ;
            } else {
                res += suf_max - height[right];
                right -- ;
            }
        }
        return res;
    }
};

13.罗马数字转整数

给你一个罗马数字，将其转换为整数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

unordered_map<char, int> ROMAN = {
    {'I', 1},
    {'V', 5},
    {'X', 10},
    {'L', 50},
    {'C', 100},
    {'D', 500},
    {'M', 1000},
};

class Solution {
public:
    int romanToInt(string s) {
        int ans = 0;
        for (int i = 0; i + 1 < s.size(); i ++ ) {
            int x = ROMAN[s[i]], y = ROMAN[s[i + 1]];
            ans += x < y ? -x : x;
        }
        return ans + ROMAN[s.back()];
    }
};

12.整数转罗马数字

给你一个整数，将其转为罗马数字

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Solution {
    static constexpr string R[4][10] = {
        {"", "I", "II", "III", "IV", "V", "VI", "VII", "VIII", "IX"}, // 个位
        {"", "X", "XX", "XXX", "XL", "L", "LX", "LXX", "LXXX", "XC"}, // 十位
        {"", "C", "CC", "CCC", "CD", "D", "DC", "DCC", "DCCC", "CM"}, // 百位
        {"", "M", "MM", "MMM"}, // 千位
    };

public:
    string intToRoman(int num) {
        return R[3][num / 1000] + R[2][num / 100 % 10] + R[1][num / 10 % 10] + R[0][num % 10];
    }
};

58.最后一个单词的长度

给你一个字符串 s，由若干单词组成，单词前后用一些空格字符隔开。返回字符串中 最后一个 单词的长度。 单词 是指仅由字母组成、不包含任何空格字符的最大子字符串。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

class Solution {
public:
    int lengthOfLastWord(string s) {
        int i = s.length() - 1;
        while (s[i] == ' ' && i > 0) i -- ;
        int j = i - 1;
        while (j >= 0 && s[j] != ' ') j -- ;
        return i - j;
    }
};

14.最长公共前缀

编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀，返回空字符串 ""。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution {
public:
    string longestCommonPrefix(vector<string>& strs) {
        string& s0 = strs[0];
        for (int j = 0; j < s0.size(); j ++ ) {
            for (string& s : strs) {
                if (j == s.size() || s[j] != s0[j]) {
                    return s0.substr(0, j);
                }
            }
        }
        return s0;
    }
};

151.反转字符串中的单词

给你一个字符串 s ，请你反转字符串中 单词 的顺序。
单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。
返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。
注意：输入字符串 s 中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中，单词间应当仅用单个空格分隔，且不包含任何额外的空格。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution {
    public String reverseWords(String s) {
        s = s.trim();                                    // 删除首尾空格
        int j = s.length() - 1, i = j;
        StringBuilder res = new StringBuilder();
        while (i >= 0) {
            while (i >= 0 && s.charAt(i) != ' ') i--;     // 搜索首个空格
            res.append(s.substring(i + 1, j + 1) + " "); // 添加单词
            while (i >= 0 && s.charAt(i) == ' ') i--;     // 跳过单词间空格
            j = i;                                       // j 指向下个单词的尾字符
        }
        return res.toString().trim();                    // 转化为字符串并返回
    }
}

28.找出字符串中第一个匹配项的下标

给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标（下标从 0 开始）。如果 needle 不是 haystack 的一部分，则返回 -1 。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Solution {
public:
    int strStr(string haystack, string needle) {

        int m = haystack.size(), n = needle.size();
        for (int i = 0; i < haystack.size(); i ++ ) {
            if (i + n > m) return -1;
            // 判断两个区间的值是否相同
            if (haystack.substr(i, n) == needle) return i;
        }
        return -1;
    }
};

双指针

11.盛水最多的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 说明：你不能倾斜容器。

123

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

// 思路和接雨水类似
class Solution {
public:
    int maxArea(vector<int>& height) {
        int n = height.size();
        int left = 0, right = n - 1;

        int ans = 0;
        while (left < right) {
            ans = max(ans, min(height[left], height[right]) * (right - left));
            if (height[left] < height[right]) {
                left ++ ;
            } else {
                right -- ;
            }
        }
        return ans;
    }
};

15.三数之和

🔗 给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。
注意：答案中不可以包含重复的三元组。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        int n = nums.size();
        vector<vector<int>> ans;

        sort(nums.begin(), nums.end());

        // 本质上是过滤所有不可能的情况

        for (int i = 0; i < n; i ++ ) {
            if (i && nums[i] == nums[i - 1]) continue;
            for (int j = i + 1, k = n - 1; j < k; j ++ ) {
                if (j > i + 1 && nums[j] == nums[j - 1]) continue;
                while (j < k - 1 && nums[i] + nums[j] + nums[k - 1] >= 0) k -- ;
                if (nums[i] + nums[j] + nums[k] == 0) ans.push_back({nums[i], nums[j], nums[k]});
            }
        }
        return ans;
    }
};

滑动窗口

209.长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 target 。 找出该数组中满足其总和大于等于 target 的长度最小的 子数组 [nums_l, nums_l+1, ..., nums_r-1, nums_r] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        // 预处理前缀和
        int n = nums.size();
        vector<int> s(n + 1, 0);
        for (int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + nums[i - 1];

        // 枚举右指针，然后移动左指针
        int l = 1;  // l 不用回头
        int ans = n + 1;
        for (int r = 1; r <= n; r ++ ) {          
            while ((s[r] - s[l - 1]) >= target) {
                ans = min(ans, r - l + 1);
                l ++ ;
            }
        }
        return ans <= n ? ans : 0;
    }
};

3.无重复字符的最长子串

给定一个字符串 s ，请你找出其中不含有重复字符的 最长 子串 的长度。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class Solution {
public:
    int lengthOfLongestSubstring(string s) {  
        // 滑动窗口,
        unordered_map<char, int> heap;  // 记录每个字符出现过多少次

        int res = 0;
        int left = 0;
        for (int i = 0; i < s.size(); i ++ ) {
            heap[s[i]] ++ ;
            while (heap[s[i]] > 1) {
                heap[s[left]] -- ;
                left ++ ;
            }
            res = max(res, i - left + 1);
        }
        return res;
    }
};

76.最小覆盖子串

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

class Solution {
    bool is_covered(int cnt_s[], int cnt_t[]) {
        for (int i = 'A'; i <= 'Z'; i ++ ) {
            if (cnt_s[i] < cnt_t[i]) {
                return false;
            }
        }
        for (int i = 'a'; i <= 'z'; i ++ ) {
            if (cnt_s[i] < cnt_t[i]) {
                return false;
            }
        }
        return true;
    }
public:
    string minWindow(string s, string t) {
        // 不定长滑动窗口
        int cnt_s[128]{};
        int cnt_t[128]{};
        int min_left = -1;
        int min_right = s.size();
        int ans = s.size();

        for (int i = 0; i < t.size(); i ++ ) cnt_t[t[i]] ++ ;
        for (int i = 0, left = 0; i < s.size(); i ++ ) {
            cnt_s[s[i]] ++ ;
            // 已经全覆盖了，右移左端点
            while (is_covered(cnt_s, cnt_t)) {
                if (i - left < min_right - min_left) {
                    min_left = left;
                    min_right = i;
                }
                cnt_s[s[left]] -- ;
                left ++ ;
            }
        }

        if (min_left >= 0) {
            return s.substr(min_left, min_right - min_left + 1);
        }
        return "";
    }
};

矩阵

54.螺旋矩阵

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

image

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        vector<int> res;

        int m = matrix.size();
        int n = matrix[0].size();

        vector<vector<int>> st(m + 10, vector<int>(n + 10, 0));

        // 用坐标偏移法模拟
        int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0};  // 右，下，左，上
        int step = 0;  // 0, 1, 2, 3

        // m 行，n 列
        st[0][0] = 1;
        res.push_back(matrix[0][0]);
        int cnt = m * n - 1;

        int i = 0, j = 0;
        while (cnt -- ) {
            int x = i + dx[step];
            int y = j + dy[step];

            // 判断将要走的点有没有越过边界
            if (x >= m || x < 0 || y < 0 || y >= n || st[x][y] == 1) {
                step = (step + 1) % 4;    
                x = i + dx[step];
                y = j + dy[step];
            }

            res.push_back(matrix[x][y]);

            i = x;
            j = y;
        }


        return res;
    }
};

48.旋转图像

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

image

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        // 先上下颠倒，再矩阵转置

        int m = matrix.size();
        int n = matrix[0].size();

        for (int i = 0; i < m / 2; i ++ ) {
            for (int j = 0; j < n; j ++ ) {
                swap(matrix[i][j], matrix[m - 1 - i][j]);
            }
        }

        // 矩阵转置通用公式
        for (int i = 0; i < m; i ++ ) {
            for (int j = i + 1; j < n; j ++ ) {
                swap(matrix[i][j], matrix[j][i]);
            }
        }
    }
};

哈希表

128.最长连续序列

给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。请你设计并实现时间复杂度为 O(n) 的算法解决此问题。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        int ans = 0;
        unordered_set<int> st(nums.begin(), nums.end());  // 把 nums 转为哈希集合
        for (int x : st) {  // 遍历哈希集合
            if (st.contains(x - 1)) {
                continue;  // 如果 x-1 在哈希集合中，则不以 x 为起点，因为 x-1 为起点计算出来的连续序列一定更长
            }
            // x 是序列的起点
            int y = x + 1;
            while (st.contains(y)) {  // 不断查找下一个数是否在哈希集合中
                y ++ ;
            }
            ans = max(ans, y - x);  // 从 x 到 y - 1 一共 y - x 个数
        }
        return ans;
    }
};

链表

92.反转链表 II

给你单链表的头指针 head 和两个整数 left 和 right ，其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点，返回 反转后的链表 。

image

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseBetween(ListNode* head, int left, int right) {
        ListNode dummy{0, head};

        ListNode* p0 = &dummy;

        // 首先维护p0指针，p0指针是待处理段的前一个指针（哨兵节点）
        for (int i = 0; i < left - 1; i ++ ) {
            p0 = p0->next;
        }

        ListNode* pre = nullptr;
        ListNode* cur = p0->next;

        for (int i = 0; i < right - left + 1; i ++ ) {
            ListNode* nxt = cur->next;
            cur->next = pre;
            pre = cur;
            cur = nxt;
        }

        p0->next->next = cur;
        p0->next = pre;

        return dummy.next;
    }
};

25.K 个一组翻转链表

🔗 给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。
k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。
你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

image

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        // 统计节点个数
        int n = 0;
        for (ListNode* cur = head; cur; cur = cur->next) n ++ ;

        ListNode dummy(0, head);  // 哨兵节点，哨兵的下一个节点是head
        ListNode* p0 = &dummy;

        ListNode* pre = nullptr;
        ListNode* cur = head;

        // k 个一组进行处理
        for (; n >= k; n -= k) {
            // 每组内部就是 反转链表II
            for (int i = 0; i < k; i ++ ) {
                ListNode* nxt = cur->next;  // cur不断往右走的同时，维护pre指针和nxt指针
                cur->next = pre;
                pre = cur;
                cur = nxt;
            }

            // 处理p0指针，p0指针主要是指向每一段被处理链表的哨兵节点（前一个节点）
            ListNode* nxt = p0->next;
            p0->next->next = cur;
            p0->next = pre;
            p0 = nxt;
        }
        return dummy.next;
    }
};

19.删除链表的倒数第 N 个结点

🔗 给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

image

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode dummy{0, head};
        ListNode* left = &dummy;
        ListNode* right = &dummy;

        // 左右指针都先往右走n步
        while (n -- ) {
            left = left->next;
            right = right->next;
        }

        // 再同时走一段距离，让右指针指向最后一个节点
        while (right->next) {
            left = left->next;
            right = right->next;
        }

        // 此时 left 下一个节点就是倒数第 n 个节点
        ListNode* nxt = left->next;
        left->next = left->next->next;

        delete nxt;
        return dummy.next;
    }
};

82.删除排序链表中的重复元素II

🔗 给定一个已排序的链表的头 head ， 删除原始链表中所有重复数字的节点，只留下不同的数字 。返回 已排序的链表

image

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
        if (head == nullptr) return nullptr;

        ListNode dummy{0, head};
        ListNode* cur = &dummy;

        while (cur->next && cur->next->next) {
            if (cur->next->val == cur->next->next->val) {
                int x = cur->next->val;
                while (cur->next && cur->next->val == x) {
                    cur->next = cur->next->next;
                }
            } else {
                cur = cur->next;
            }
        }
        return dummy.next;
    }
};

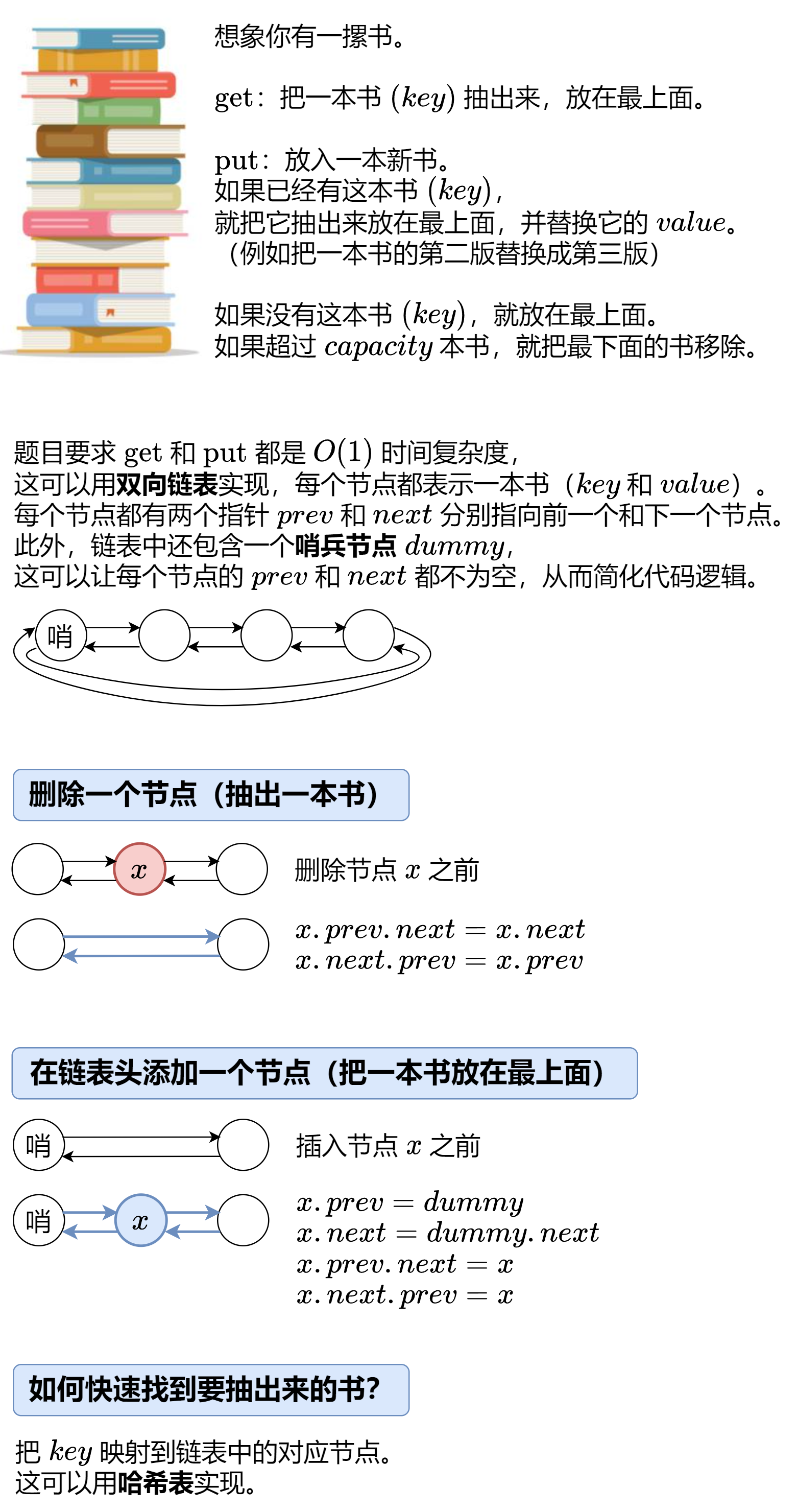
146.LRU 缓存

🔗 请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类：

  • LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
  • int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
  • void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

用图巧记

image

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

struct Node {
    int key;
    int value;
    Node* prev;
    Node* next;

    Node(int k = 0, int v = 0) : key(k), value(v) {}
};

class LRUCache {
private:
    int capacity;
    Node* dummy;
    unordered_map<int, Node*> key_to_node;

    void remove(Node* x) {
        x->prev->next = x->next;
        x->next->prev = x->prev;
    }

    void push_front(Node* x) {
        x->next = dummy->next;
        x->prev = dummy;
        x->prev->next = x;
        x->next->prev = x;
    }

    Node* get_node(int key) {
        auto it = key_to_node.find(key);
        if (it == key_to_node.end()) return nullptr;
        Node* node = key_to_node[key];
        remove(node);
        push_front(node);
        return node;
    }

public:
    LRUCache(int capacity) : capacity(capacity), dummy(new Node()) {
        dummy->prev = dummy;
        dummy->next = dummy;
    }

    int get(int key) {
        Node* node = get_node(key);
        return node ? node->value : -1;
    }

    void put(int key, int value) {
        Node* node = get_node(key);
        if (node) {
            node->value = value;
            return;
        }
        node = new Node(key, value);
        key_to_node[key] = node;
        push_front(node);

        if (key_to_node.size() > capacity) {
            Node* back_node = dummy->prev;
            key_to_node.erase(back_node->key);
            remove(back_node);
            delete back_node;
        }
    }
};

堆

215.数组中的第K个最大元素

🔗 给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。
请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution {
public:
    int findKthLargest(vector<int>& nums, int target) {
        // 第 K 个最大元素
        // 1 2 3 4，n=4, K=2，则
        auto quick_select = [&](this auto&&quick_select, int l, int r, int k) {
            if (l >= r) return nums[l];

            int x = nums[(l + r) / 2], i = l - 1, j = r + 1;
            while (i < j) {
                do i ++ ; while (nums[i] < x);
                do j -- ; while (nums[j] > x);
                if (i < j) swap(nums[i], nums[j]);
            }
            int sl = j - l + 1;
            if (k <= sl) return quick_select(l, j, k);
            return quick_select(j + 1, r, k - sl);
        };

        int n = nums.size();

        return quick_select(0, n - 1, n - target + 1);
    }
};

295.数据流的中位数

🔗 中位数是有序整数列表中的中间值。如果列表的大小是偶数，则没有中间值，中位数是两个中间值的平均值。

  • 例如 arr = [2,3,4] 的中位数是 3 。
  • 例如 arr = [2,3] 的中位数是 (2 + 3) / 2 = 2.5 。
    实现 MedianFinder 类:
  • MedianFinder() 初始化 MedianFinder 对象。
  • void addNum(int num) 将数据流中的整数 num 添加到数据结构中。
    double findMedian() 返回到目前为止所有元素的中位数。与实际答案相差 10^-5 以内的答案将被接受。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

class MedianFinder {
    priority_queue<int, vector<int>, greater<int>> up;  // 小根堆
    priority_queue<int> down;  // 大根堆
    int siz;
public:
    MedianFinder() {
        siz = 0;  // 记录对顶堆中元素大小
    }

    // 对顶堆维护动态中位数

    void addNum(int num) {
        if (down.empty() || num <= down.top()) down.push(num);
        else up.push(num);

        siz ++ ;

        if (down.size() > up.size() + 1) up.push(down.top()), down.pop();
        if (up.size() > down.size()) down.push(up.top()), up.pop();
    }

    double findMedian() {
        if (siz % 2) return down.top();
        return (up.top() + down.top()) / 2.0;
    }
};

/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder* obj = new MedianFinder();
 * obj->addNum(num);
 * double param_2 = obj->findMedian();
 */

一维动态规划

139.单词拆分

🔗 给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。
注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

这里用到了字符串哈希来优化

这里有一个隐藏的细节是 “秦九韶算法”，即哈希值的维护。如果不这样写则需要维护一个 p 数组，来进行 a*P^3 + b*P^2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        typedef unsigned long long ULL;  // 用ULL表示是因为为了对 2^64 取模
        unordered_set<ULL> hash;
        const int P = 131;  // P进制的经验值，也可以取 13331，可以认为99%的概率不会哈希冲突

        for (auto& s : wordDict) {
            ULL h = 0;
            for (auto c : s) {
                h = h * P + c;  // 将词表中的每个词映射至 P 进制，秦九韶算法写法；
            }
            hash.insert(h);
        }

        int n = s.size();
        vector<bool> f(n + 1);

        s = " " + s;
        f[0] = true;  // f[i]表示单词 s 的前 i 个字符能否由 wordDict 中的单词组成，其中边界 f[0] = true
        for (int i = 0; i < n; i ++ ) {
            if (f[i]) {  // 如果 f[i] = true 并且 s[i + 1:j] 也在 wordDict 中，则 f[j] = true
                ULL h = 0;
                for (int j = i + 1; j <= n; j ++ ) {  // 查询 s[i + 1:j] 中所有的字符串是否在 wordDict 中出现过
                    h = h * P + s[j];
                    if (hash.count(h)) f[j] = true;  
                }
            }
        }
        return f[n];
    }
};

多维动态规划

120. 三角形最小路径和

🔗 给定一个三角形 triangle ，找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class Solution {
public:
    int minimumTotal(vector<vector<int>>& grid) {
        int n = grid.size();
        const int INF = 0x3f3f3f3f;

        vector<vector<int>> f(n + 1, vector<int>(n + 1, -1));

        auto dfs = [&](this auto&& dfs, int x, int y) {
            int n = grid.size();

            if (x == n - 1) return f[x][y] = grid[x][y]; // 不能继续走，f[x][y]的值就是当前点的值
            if (f[x][y] != -1) return f[x][y];


            int res = INF;
            if (x >= 0 && x < n && y >= 0 && y <= x) {

                res = min(dfs(x + 1, y), dfs(x + 1, y + 1)) + grid[x][y];
            }

            return f[x][y] = res;
        };
        return dfs(0, 0);
    }
};

221.最大正方形

🔗 在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内，找到只包含 ‘1’ 的最大正方形，并返回其面积。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution {
    static const int N = 310;
    int f[N][N];
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();

        memset(f, 0, sizeof f);

        int a = 0;
        for (int i = 0; i < m; i ++ ) {
            for (int j = 0; j < n; j ++ ) {
                if (matrix[i][j] == '0') continue;
                if (i == 0 || j == 0) f[i][j] = 1;  // 边长最大只能为1
                else {
                    // f[i][j]表示以 (i,j) 为右下角的，最大正方形的边长
                    f[i][j] = min(min(f[i][j - 1], f[i - 1][j]), f[i - 1][j - 1]) + 1;
                }
                a = max(a, f[i][j]);
            }
        }
        return a * a;
    }
};
更新于 2025-03-24 
CC BY-NC 4.0
阅读原始文档
算法
返回 | 主页
yitao 支付宝支付宝
yitao 微信微信
0%