量化
基本概念
缩放系数:$s= \dfrac{r_{max} - r_{min}}{q_{max} - q_{min}} = \dfrac{\max(|r_{min}|, |r_{max}|)}{2^{N-1}}$
零点:$z=round(q_{min}-\dfrac{r_{min}}{s})=round(-2^{N-1}-\dfrac{r_{min}}{s})$
这里 $r_{min}$ 指的是输入值的最大和最小值。$q_{min}, q_{max}$ 是指量化后的整数范围。
| |
这里有个前置知识就是,在神经网络中一般权重的形状 都是 $W\in R^{O\times I}$,其中 $O$ 表示输出通道(output channel), $I$ 表示输入通道(input channel),对于矩阵乘法,即 $y = Wx$, $x\in R^{I}, y\in R^{O}$
数值精度
常用浮点数精度:
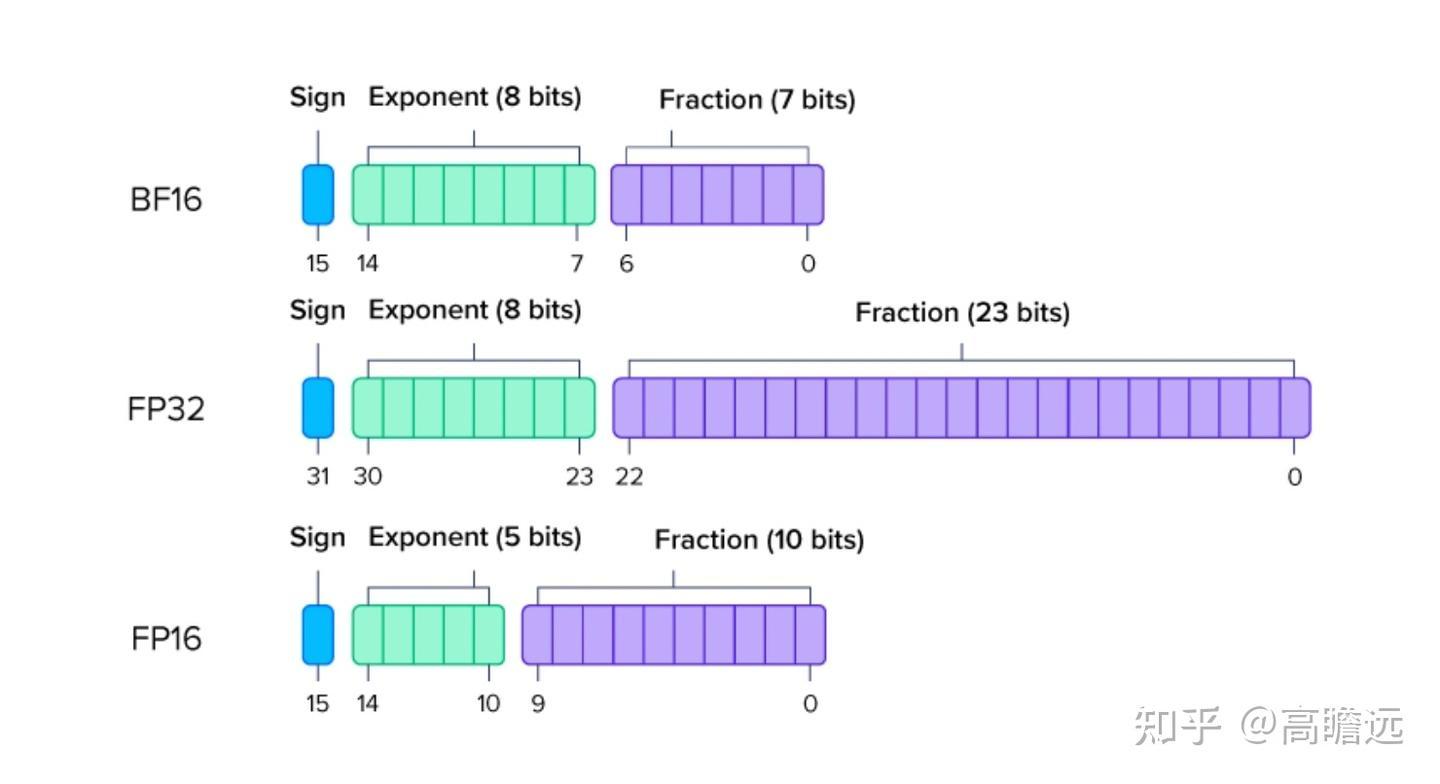
FP8 E4M3 FP8 E5M2
W4A16 在大batch和小batch的场景中起作用的方式
场景一:大 Batch (Large Batch Size)
这种场景常见于离线推理、批处理任务,目标是最大化吞吐量 (Throughput),即单位时间内处理的样本总数(QPS, Queries Per Second)。
核心瓶颈:内存带宽 (Memory-Bound)
当 Batch Size 很大时,输入激活值的矩阵(形状如 [Batch Size, Seq Length, Hidden Dim])变得非常“厚”。此时,GPU 需要处理的计算量(FLOPs)极大,为了完成这些计算,它必须不断地从速度较慢的显存(VRAM)中把巨大的权重矩阵加载到速度极快的缓存(SRAM)和计算单元中。
由于权重矩阵非常庞大(例如,Llama 70B 的权重超过 100GB),加载权重所花费的时间远远超过了实际计算的时间。这时,我们就说系统是 “内存带宽受限” (Memory-Bound) 的。
W4A16 如何起作用:
极大缓解内存带宽瓶颈:这是 W4A16 在大 Batch 场景下最核心的优势。
权重以 4-bit 形式存储在显存中,体积是 FP16 的 1/4。
从显存加载到高速缓存时,数据传输量只有原来的 1/4,加载时间也相应大幅缩短。
这意味着 GPU 等待数据的时间大大减少,计算单元可以更快地被“喂饱”,从而提升了整体的运行效率。
反量化开销被摊销 (Amortized Overhead):
虽然 4-bit 权重需要一个额外的反量化步骤(W4 -> W16),这个操作本身是有开销的。
但在大 Batch 场景下,这个开销被摊薄了。你只需要反量化一次权重矩阵,就可以用它来处理 Batch 中成百上千个样本。
相比于从内存带宽上节省的大量时间,这点反量化的计算开销几乎可以忽略不计。
结论: 在大 Batch 场景下,W4A16 规格能显著提升吞吐量。其主要作用是通过压缩权重来降低对内存带宽的压力,让 GPU 的计算核心能够火力全开。
场景二:小 Batch (Small Batch Size, e.g., Batch Size = 1)
这种场景常见于在线服务、实时交互式应用(如聊天机器人),目标是最小化延迟 (Latency),即处理单个请求所需的时间。
核心瓶颈:计算延迟与固定开销 (Compute-Bound / Overhead-Bound)
当 Batch Size 很小时(尤其是 1),输入激活值的矩阵变得非常“薄”。GPU 需要执行的计算量相对较小。此时,加载权重的时间虽然也存在,但它在总耗时中的占比已经不像大 Batch 场景那么极端。
系统的瓶颈转变为计算单元执行计算本身的速度以及各种固定开销,例如 Kernel Launch(启动计算核心)的延迟、反量化操作的延迟等。这时,系统更偏向于 “计算受限” (Compute-Bound)。
W4A16 如何起作用:
内存带宽优势减弱:
- 虽然加载 W4 权重依然比加载 W16 权重快,但因为总的计算量很小,这部分节省的时间在总延迟中的占比也变小了,优势不再那么明显。
反量化开销变得显著:
关键区别在于,反量化的开销无法被摊销。你为单个样本的单次计算,完整地承受了“权重加载 + 权重反量化”的全部开销。
这个固定的开销在总耗时中占了更高的比例。在某些情况下,反量化带来的额外计算时间,甚至可能超过因权重压缩节省下来的内存加载时间。
主要收益变为显存占用:
在小 Batch 场景下,W4A16 带来的最大好处,从“提升性能”转向了“降低显存占用”。
它使得原本需要大量显存才能装载的大模型(如 70B 模型需要 >140GB FP16 显存),现在可以在显存较小的硬件上(如单张 40GB/80GB 的 A100/H100)运行起来。这是“能不能跑”的问题,而不是“跑多快”的问题。
结论: 在小 Batch 场景下,W4A16 对降低延迟的效果不确定,有时甚至会因为反量化开销而轻微增加延迟。它最主要的作用是大幅降低了模型的显存门槛,让大模型能够在更多硬件上部署。对于追求极致低延迟的场景,有时专门优化的 INT8(W8A8)方案可能表现更佳。
| 特性 | 大 Batch 场景 (高吞吐量) | 小 Batch 场景 (低延迟) |
|---|---|---|
| 核心瓶颈 | 内存带宽 (Memory-Bound) | 计算延迟 / 固定开销 (Compute/Overhead-Bound) |
| W4 (权重) 的作用 | 效果极佳。4-bit 权重极大缓解内存带宽瓶颈,因为加载权重的时间是主要耗时。 | 效果一般。加载权重的时间占比下降,优势减弱。 |
| A16 (激活) 的作用 | 保持模型精度,对性能影响不大。 | 保持模型精度,对性能影响不大。 |
| 反量化开销 | 可摊销。一次反量化服务于大量数据,开销占比极低。 | 显著。固定开销在单次计算中占比更高,可能抵消带宽优势。 |
| 主要收益 | 显著提升吞吐量 (QPS)、降低显存占用。 | 主要是降低显存占用,对延迟的改善不确定,有时甚至会劣化。 |
| 适用性 | 非常适合离线推理、批处理任务。 | 适用于需要部署超大模型但显存有限的场景,但需仔细评估延迟。 |
量化粒度 - 三种形式
- per-tensor
这是最粗粒度的量化方式。对整个 tensor 计算出一个统一的缩放因子(scale factor),然后将张量中的所有元素都使用这个缩放因子量化到低精度格式,例如 INT8。例如,一个 INT8 的 per-tensor 动态量化器会找到整个张量的最大绝对值,以此计算出一个缩放因子,然后将所有元素缩放到 INT8 的表示范围内 [-127, +127] 并进行取整1 。
- per-token
这种量化方式的粒度比 per-tensor 更细。对于张量的每一个 token(通常指的是矩阵的每一行),都单独计算并应用一个缩放因子。
- per-block
这种量化方式的粒度比 per-token 更细。它将张量在 token 维度上划分为若干个块(block)。对于每一个块内的所有 token(行),计算出一个统一的缩放因子并应用,。
- per-channel
这种量化方式和 per-token 类似,但是量化维度不一样,对于张量的每一个通道(通常指 hidden dim 维度的一列),都单独计算并应用一个缩放因子。
离群值 (Outliers)
离群值的存在是模型量化时精度下降的主要原因。这是因为量化将模型中的连续数值映射到有限的离散数值范围(例如 INT4 的范围是 [-7, +7])。如果数据中存在少数数值远超其他数据的离群值,为了表示这些极端的数值,量化的步长(resolution)就需要增大。
这样做的直接后果是:
大多数正常的、幅度较小的数值在量化后会变得非常接近甚至等于零。例如,如果一个数值比组内的最大值小很多倍,它可能会被量化为零,导致大量信息的丢失。
有限的量化比特无法精确表示这些大部分的正常数值,从而降低了整体的量化精度。
为了解决这个问题,需要采用平滑(smoothing)技术来减小激活或权重中离群值的影响,使得数值的幅度分布更加均匀。量化方法通过观察任务的 outliner 特点,来针对性地设计量化方法。
比较有代表性的是SmoothQuant ,它观察到在LLM的推理过程中,激活值(activations)中往往比权重值(weights)更容易出现显著的离群值。SmoothQuant 通过一种数学上等价的Per-channel缩放(channel-wise scaling)操作,将模型量化的难度从激活转移到权重。具体来说,它降低了激活中异常大的数值,使得激活值更容易被量化到低比特(例如 INT8),从而在保持模型精度的前提下,实现更高效的量化推理。
对称 / 非对称量化区别
| 项目 | 对称量化 | 非对称量化 |
|---|---|---|
| 是否有 zero point | ❌ 固定为 0 | ✅ 存在 zero_point |
| 适用范围 | 权重量化(特别是 centered) | 激活量化(值范围变化大) |
| 运算简化 | ✅ 快速,适合矩阵乘法 | ❌ 多了减法,加快复杂度 |
| 表现力 | ❌ 表达负偏移有限 | ✅ 支持偏移,精度更高 |
| 效果稳定性 | ✅ 稳定 | ✅ 更灵活,适应动态变化 |
量化对象
Linear(Dense) 量化
指对模型的 Linear 层进行量化,Linear 层主要分布于:
- Attention 中的 Q/K/V/O projection
- MLP(FFN) 中的 gate/up/down
- Embedding (
[vocab_size, hidden_size]) 和 LM Head ([hidden_size, vocab_size]) - MoE 中的 expert
Attention量化,以 SageAttention 为例
首先 SageAttention 是基于 FlashAttention2并采用动态量化。
SageAttention 基于 FlashAttention 的分块方法,对分块应用per-block的方式进行量化。具体来说,在Q,K,P,V的分块上进行 INT8 量化,然后对乘积进行反量化,主要是为了加速 QK^T 和 PV 的矩阵乘法计算。online softmax 保持全精度。
per-block 量化
“块”(block)是指将输入张量按序列维度划分的连续数据段。每个块包含固定数量的 token,对整个块使用同一个量化缩放因子。用一个具体的例子说明:
假设我们有一个 Query 张量,形状为 [1, 8, 512, 128](batch=1, heads=8, seq_len=512, head_dim=128),使用 BLKQ=128 的块大小:
- 序列长度 512 被划分为 512 ÷ 128 = 4 个块
- 第1块:token 0-127
- 第2块:token 128-255
- 第3块:token 256-383
- 第4块:token 384-511
对于上述例子,Q 的缩放因子张量形状为 [1, 8, 4],即每个 head 的每个块都有一个缩放因子。
Smooth-K
K表现出明显的 Channel 方向异常值,但是由于矩阵乘法 $QK^T$ 中,量化只能在token维度上进行,因此无法对K应用per-channel量化。
但是K的通道异常值表现出一个规律,即每个token的key实际上是所有tokens共享的一个大bias,再加上一个小的token-wise的信号。
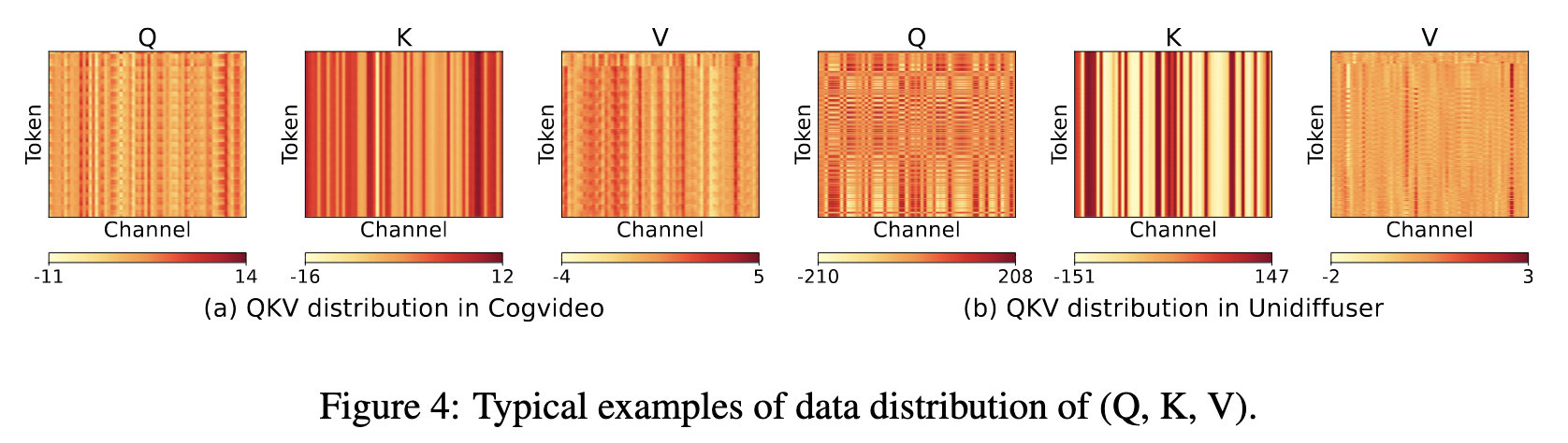
即在最终量化之前,先从全精度 K 中减去平均值。
Quantization for Q, K, P, V
- Q, K 的量化粒度:Q和K的量化粒度可以设置为 per-token,per-block或per-tensor粒度。但是不可以设置为 per-channel,原因上面说了,内轴在相乘时会约掉,没办法进行反量化
- Q, K的数据类型:之所以对Q和K进行 INT8 量化,原因有两个:其一是因为测试了很多模型,对Q,K,P,V使用INT8 量化比 FP8量化具有更高的准确率;其二是因为在许多常用的GPU上进行INT8矩阵乘法比使用FP8快两倍
- P, V的量化粒度:对P进行per-block量化,对V进行per-channel量化,原因有三个:其一是因为对P进行per-channel量化和对V进行per-token量化不可行,因为反量化需要外部轴的scale factor;其二是P的每一行最大值为1,因此可以为一个块分配一个固定的scale factor $s=\frac{1}{127}$;其三是per-channel量化可以解决V的通道方向异常值问题
FP16 累加
对 P和V进行量化时,在某些模型层使用INT8的准确率会非常低。
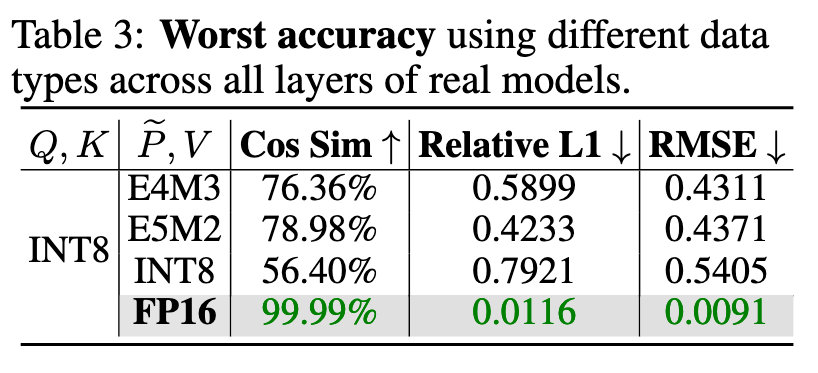
论文中建议在矩阵乘法PV中使用FP16作为数据类型,并且使用FP16累加器
使用 FP16 累加器的 FP16 矩阵乘法速度比使用 FP32 累加器快 2 倍。此外,使用 FP16 累加器比使用 FP32 累加器可以节省更多的寄存器资源,从而加快计算速度。其次,表 3 表明,对 P, V 使用 FP16 比使用所有其他 8 位数据类型要精确得多。而且,使用 FP16 累加器与使用 FP32 累加器相比不会导致精度损失。
关于内部轴不可进行反量化的分析
矩阵乘法中,对于每个矩阵你只能沿着公共维度进行量化(下图右边)。根据这个简单的原则,Attention 中四个矩阵可以量化的组合如下。注意能做 per-token,就能做 per-block 量化。其中 P 代表 $softmax(QK^T/\sqrt{d})$
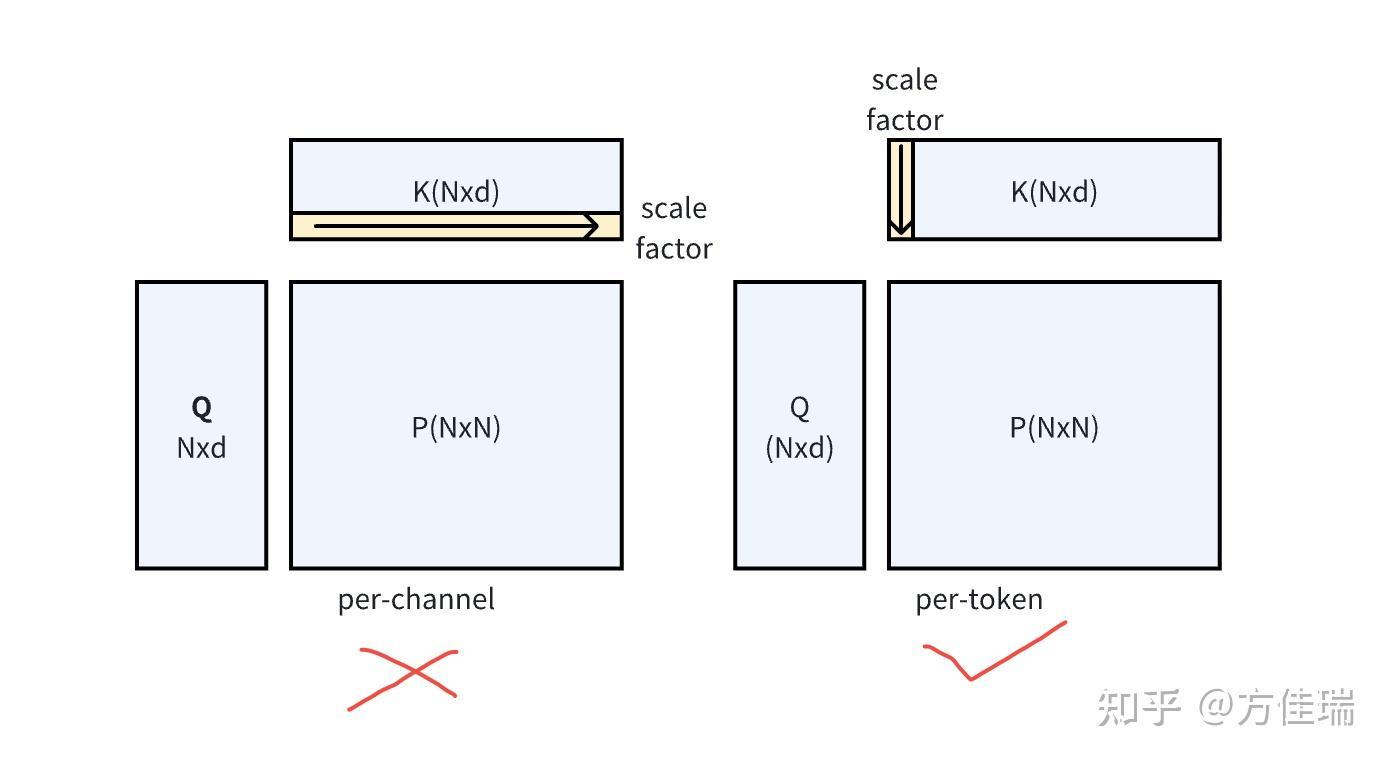
这是因为在进行矩阵乘法 $QK^{T}$ 后,得到的结果矩阵的维度是 N × N(Q 和 K 的维度都是 N × d)。如果我们对 K 进行了per-channel 量化(下图左边,总共 d 个channel,每个 channel 包含 N 个元素),每个通道都有一个独立的scale factor,总共是 d 个 scale factor。在反量化(dequantization)时,我们需要将量化后的结果乘以对应的scale factor,而QK^T 的结果矩阵的维度是 NxN,根本没有 d 的通道维度不直接对应,因此无法使用 K 的通道维度的缩放因子进行正确的反量化。
| Q | K | P | V | |
|---|---|---|---|---|
| per-channel | ❌ | ❌ | ❌ | ✅ |
| per-token | ✅ | ✅ | ✅ | ❌ |
| per-block | ✅ | ✅ | ✅ | ❌ |
量化类型
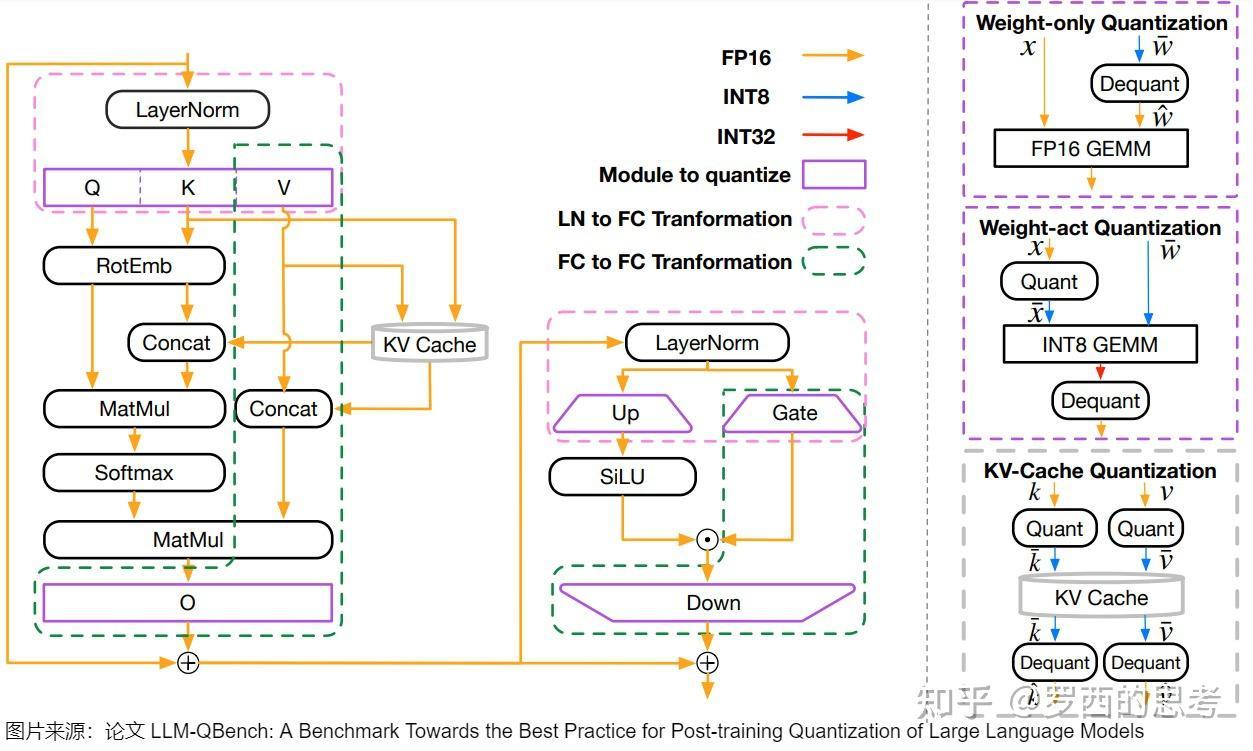
INT 量化范式:
- FP32作为基准,提供了最大的数值范围和零精度损失,但存储开销最大。
- 如果用户不太关心效率,那么INT16格式是最佳选择。INT16格式是最精确的,如果是转换FP32,INT16甚至比FP16更精确。
- 对于对实时性要求高的服务,建议采用INT8量化方案,可以在保持较高精度的同时获得显著的性能提升。如果你的网络中某些层需要更高的精度,可以使用W8A16来解决这个问题。
- 在资源受限但对精度要求相对较低的场景,则可以采用INT4方案以获得最大的资源效益。
weight-only
GPTQ
$\text{Frobenius}$ 范数,简称 F-范数,$||\cdot||^{2}_{2}$ 表示对矩阵的 Frobenius 范数的平方(即所有元素平方和) Frobenius 范数可以用来衡量矩阵整体的大小,比如在误差分析中,可以用来评估两个矩阵之间的差异程度
GPTQ是一种训练后权重量化方法,使用基于二阶信息的逐层量化,成功将每个权重量化至 3-4 位,几乎没有精度损失。GPTQ 对某个 block 内的所有参数逐个量化,每个参数量化后,需要适当调整这个 block 内其他未量化的参数,以弥补量化造成的精度损失。 GPTQ 量化需要准备校准数据集。
OBS/OBQ/GPTQ等一系列工作的核心就是:
不直接最小化权重误差,而是:$\min_{q(w)}||(q(w)-w)X||^2_{2}$
给定权重矩阵W,有以下步骤:
- 收集激活样本(校准数据集)
- 计算输入协方差矩阵 $H = X^{T}X$
- 逐列量化 W 的每一列
- 每列权重找最优 int4 表示
- 误差反馈,用 Hessian 更新下列的残差
- 保存量化结果,然后在推理阶段使用 int4 ✖️ float16 / int8的高效矩阵乘法



AWQ
参考:https://www.zhihu.com/search?type=content&q=AWQ%20%E9%87%8F%E5%8C%96
AWQ观察到权重通道对性能的重要性各不相同,通过保留1%的显著权重可以大大减少量化误差。基于此观察,AWQ采用了激活感知权重量化来量化LLM,具体会专注于激活值较大的权重通道,并通过每通道缩放实现最佳量化效果。
误区:AWQ量化=W4A16量化
AWQ是一种对模型权重进行低比特量化的方法,使用该方法可以将模型权重(Weight)量化为4bit,并在计算激活值(Activation)时反量化为FP16,即W4A16。也可以基于AWQ方法将权重量化为3bit/8bit,并在计算时是使用4bit/8bit/16bit,由此衍生出W4A4、W4A8等一系列方法。 作者在原文中指出,W4A16可以在精度损失较小的情况下,大幅降低内存占用,且提升模型推理速度,是最常用的方法,因此AWQ和W4A16同镜率较高。
显著权重(权重并不同等重要,仅有部分显著权重对结果影响较大)
权重矩阵中显著权重位于哪个通道,找到这个通道,将这个通道内的部分保留原来的精度(fp16),然后其他部分量化为低 bit。
步骤:在计算时,首先将激活值对每一列求绝对值的平均值,然后把平均值较大的一列对应的通道视作显著通道,保留FP16精度。对其他通道进行低比特量化,如下图:
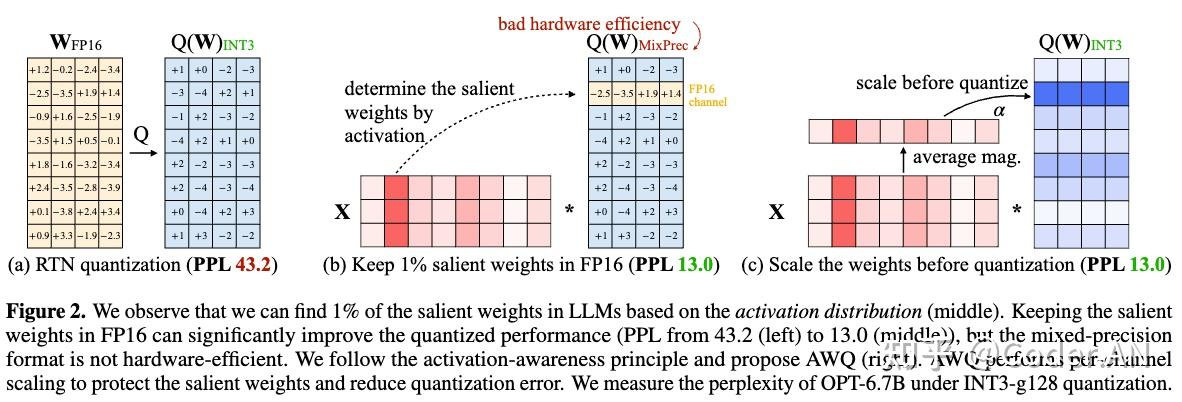
这里详细解释一下“将激活值对每一列求绝对值的平均值,然后把平均值较大的一列对应的通道视作显著通道”
对于 $y=xW^{T}$,其中 $y\in R^{B\times O}, W\in R^{O\times I}, x\in R^{B\times I}$
(这里 chatgpt 的解释是,在数学上 $y = Wx$,实现中记为 $y=xW^{T}$)
这张图中的 $X\in R^{I\times B}, W\in R^{O\times I}$,因此 $y=Wx \in R^{O\times B}$
所以不管数学上的表达还是实际上的代码实现,y 的输出通道始终由权重的输出通道决定,即 y 的输出通道是否是显著值,就看对应的激活值那一列,所以这里是求的每一列的绝对值的平均值,把平均值较大的一列视为显著通道。
但是如果这样做,权重矩阵中有的元素需要用 FP16,而其他元素需要用 INT8,不好写 kernel。因此就引入了 Scaling 方法
Scaling(量化时对显著权重进行放大可以降低量化误差)
量化误差主要来源于对权重的量化,AWQ的目标是通过缩放显著权重,减少量化误差
核心思想:对显著权重按比例放大,然后在计算时相应地缩小输入,这样在量化过程中显著权重的相对误差被降低。
量化函数(这里量化函数不是表示量化后的整数值,而是指 反量化之后的近似权重值,是直接给出最终用于推理的值):
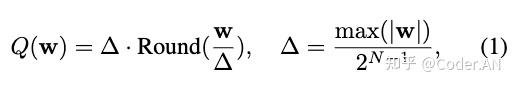
其中 $N$ 是量化后的比特数,$\Delta$ 是量化因子(scaler),$\Delta= \dfrac{max(|w|)}{2^{N-1}}$
- $w'=Round(\frac{w}{\Delta})$ 是量化过程,
- $\Delta\cdot w'$ 是反量化过程
- $w, \Delta, x$ 都是 fp16 格式,不会带来精度损失,精度损失全部来源于 round 函数
对于权重 $\text{w}$ 中的单个元素 $w$,引入一个缩放因子 $s>1$,量化过程将 $w$ 与该因子相乘,写作:$\text{w}'=Round(\dfrac{ws}{\Delta'})$,相应将反量化过程写作 $\dfrac{\Delta' \cdot w'}{s}$,对 x 进行逆缩放,则:
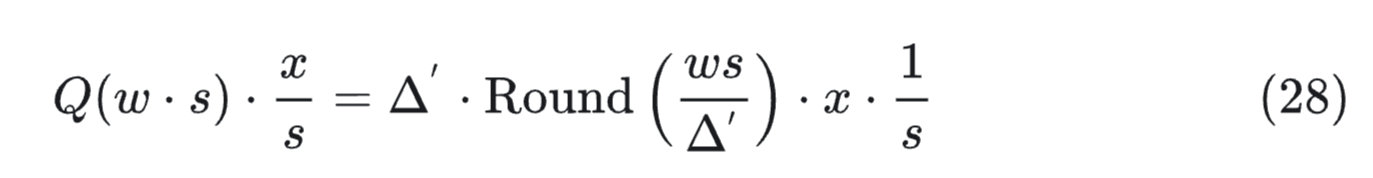
其原始量化误差为:
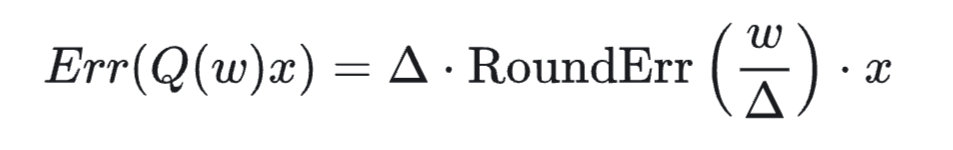
RoundErr:四舍五入误差,为±0.5
$\Delta$:量化比例因子,决定误差绝对值大小
缩放后的量化误差:
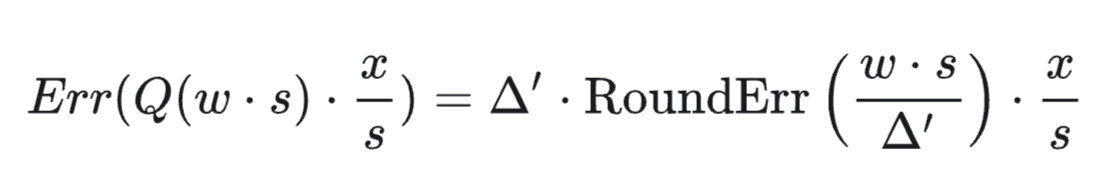
所以误差比值可以描述为 $\dfrac{\Delta'}{\Delta}\cdot \dfrac{1}{s}$,我们认为 $\Delta'\approx \Delta$,加上 $s>1$,所以作者认为量化时对显著权重进行放大,可以降低量化误差
从量化函数来看,AWQ 属于对称量化。这里量化因子 q_scale: $\Delta' = \dfrac{max(|w|)}{2^{N-1}}$
自动计算缩放系数
按照上文的分析,我们需要找到权重矩阵每个通道的缩放系数,使得量化误差最小,即最小化公式4:
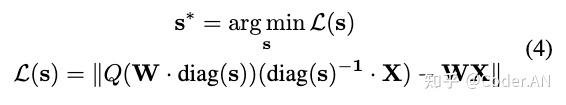
按照作者的观点,激活值越大,对应通道越显著,就应该分配更大的缩放系数降低其量化误差。这里为了简单记忆,作者统计了各通道的平均激活值(计算输入矩阵各列绝对值的平均值),并直接将此作为各通道的缩放系数。
SmoothQuant
是一个 W8A8 算法,本质还是跟 AWQ 有点像,主要是将 激活量化 的难度转移到权重上,简单来说就是 除以一个值,然后权重乘以一个值:
$$ Y=(X*\text{diag}(s)^{-1})*(\text{diag}(s)*W) $$也就是对activate (也就是X)进行缩放,并把相反的缩放系数应用到对应的weight(也就是W)上,得到数学上等价的结果。它的核心观察在于:
- 由于activation outlier的存在,activation的分布非常不规则;
- weight分布均匀 这样,通过上面的操作,试图把 activation 变得更均匀,而把 weight 的均匀分布变得没有那么均匀,也就是把activation 量化de 难度部分平摊到weight 上
并且该论文主要实现了三种量化方法:per-tensor、per-token、per-channel。同时也进行了static 和 dynamic量化的区分
weight-activation
- LLM.int8() 发现激活中的异常值集中在一小部分通道中。基于这一点,LLM.int8() 根据输入通道内的离群值分布将激活和权重分成两个不同的部分。包含激活值和权重的异常数据的通道以FP16格式存储,其他通道则以INT8格式存储。
KV cache
待补充
动态量化与静态量化
- dynamic:在线运行的时候统计缩放系数
动态离线量化仅将模型中特定算子的权重从FP32类型映射成 INT8/16 类型,bias和激活函数 在推理过程中动态量化。但是对于不同的输入值来说,其缩放因子是动态计算的(“动态”的由来)。动态量化是几种量化方法中性能最差的。
- static:离线使用标定数据计算好缩放系数
静态离线量化使用少量无标签校准数据,采用 KL 散度等方法计算量化比例因子。静态量化(Static quantization)与动态量化的区别在于其输入的缩放因子计算方法不同,静态量化的模型在使用前有“calibrate”的过程(校准缩放因子):准备部分输入(对于图像分类模型就是准备一些图片,其他任务类似),使用静态量化后的模型进行预测,在此过程中量化模型的缩放因子会根据输入数据的分布进行调整。一旦校准完成后,权重和输入的缩放因子都固定(“静态”的由来)。静态量化的性能一般比动态量化好,常用于中等模型和大模型。因此实际中基本都是在用静态量化。 网址静态离线量化的目标是求取量化比例因子,主要通过对称量化、非对称量化方式来求,而找最大值或者阈值的方法又有MinMax、KLD、ADMM、EQ等方法
支撑量化的一些算子和库
Marlin
支持混合精度运算,例如 FP16 * INT4 运算,FP8 * INT4运算
一种支持 W4A16的 GEMM kernel(一定程度上kernel 实现和量化算法是独立的),因此 marlin kernel 也支持 AWQ 量化模型执行。原始的Marlin Kernel只支持W4A16计算模式,而 QQQ 在 Marlin kernel 的基础上,支持了 W4A8 的计算模式。
MoE量化
以实习期间做过的 MoE wna16marlin kernel 为例(sgl PR 7683)
- MoE 专用路由: 支持动态专家选择和 token 路由
- 多量化格式: 支持 INT4/INT8/FP8 等多种量化类型
- Tensor Core 优化: 使用 CUDA tensor core 指令加速矩阵运算
- 内存布局优化: 针对 MoE 访问模式优化的内存布局
- 原子操作: 支持原子加法减少全局归约开销
 支付宝
支付宝 微信
微信