并查集

yitao 收录于算法

2025-08-16 约 500 字预计阅读 1 分钟

适用场景

1、将两个集合合并

2、询问两个元素是否在一个集合当中

3、维护一个集合中的点的个数：siz[root]，见 AcWing 837. 连通块中点的数量

4、维护一个集合中各个点到根节点的距离：d[]，见： AcWing 240. 食物链

核心操作：路径压缩和按秩合并（按秩合并不常用，这里省略）

上述两个操作最坏情况下为 $O(\log n)$

1
2
3
4
5
int find(int x)
{
    if (p[x] != x)  p[x] = find(p[x]);
    return p[x];
}

算法原理 & 实现

每个集合用一棵树来表示，数根的编号就是整个集合的编号，每个节点存储它的父节点，p[x]表示x的父节点。

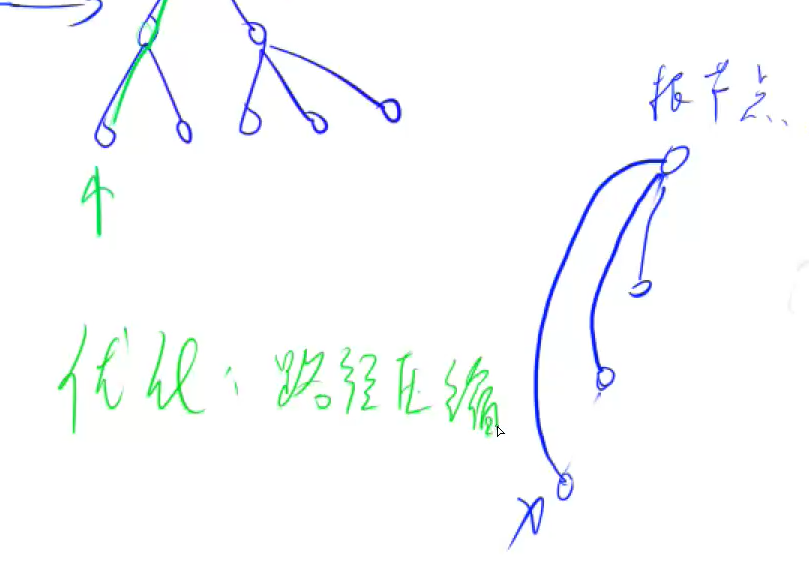
QQ截图20210629135632.png

问题1：如何判断树根？

1
if (p[x] == x)

问题2：如何求x的集合编号？

1
2
while (p[x] != x)
    x = p[x];

问题3：如何合并两个集合？

p[x] 是 x 的集合编号，p[y]是 y的集合编号。

1
p[x] = y

初始化

初始时，每个点都是一个集合，故每个点的树根就是它本身。

1
2
for (int i = 1; i <= m; i ++ )  
    p[i] = i;

完整代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>

using namespace std;

const int N = 1e5 + 10;
int p[N], n, m;

int find(int x)
{
    if(p[x] != x)  p[x] = find(p[x]);
    return p[x];
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <=m ; i ++ ) p[i] = i;

    while (m -- )
    {
        char op[2];
        int a, b;
        scanf("%s%d%d", op, &a, &b);

        if (op[0] == 'M')  p[find(a)] = find(b);
        else
        {
            if (find(a) == find(b))  puts("Yes");
            else puts("No");
        }
    }
    return 0;
}

赞赏

支付宝

微信