Softmax与Flash-Attention
safe-softmax 推导
原始的 softmax 公式:
$$ softmax(x_i) = \dfrac{exp(x_i)}{exp(x_0) + exp(x_1) + ... + exp(x_n)}$$为了防止数值溢出,超过一定范围精度下降,需要减去 $x$ 中最大值:
$$ safe-softmax(x_i) = \dfrac{exp(x_i - \max_x)}{exp(x_0 - \max_x) + exp(x_1 - \max_x) + ... + exp(x_n - \max_x)}$$该式与原始版本完全相同,因为:
$$ \begin{aligned} safe-softmax(x_i) &= \dfrac{exp(x_i - \max_x)}{exp(x_0 - \max_x) + exp(x_1 - \max_x) + ... + exp(x_n - \max_x)} \\\\ &= \dfrac{exp(x_i) / exp(\max_x)}{exp(x_0) / exp(\max_x) + exp(x_1) / exp(\max_x) + ... + exp(x_n) / exp(\max_x)} \\\\ &= \dfrac{exp(x_i)}{exp(x_0) + exp(x_1) + ... + exp(x_n)} \\\\ &= softmax(x_i) \end{aligned} $$online-softmax 推导
- $m_j = \max(m_{j-1}, x_j)$【最大值的更新】
- $d_j = e^{x_1 - m_j} + e^{x_2 - m_j} + ... + e^{x_j - m_j}$【指数和的更新】
以上,$m_j$ 为 前 j 项的最大值,$d_j$ 则代表前 j 个元素的指数和,之所以减去 $m_j$ 是因为 safe-softmax 的缘故
第一项比较好理解,第二项需要我们拆开分析:
将 $d_j = e^{x_1 - m_j} + e^{x_2 - m_j} + ... + e^{x_j - m_j}$ 的贡献拆分为:
前 j-1 项贡献:
$$e^{x_1 - m_j} + e^{x_2 - m_j} + ... + e^{x_{j-1} - m_j}$$第j项的贡献:
$$ e^{x_j - m_j} $$其中对于前j-1项的贡献,这部分指数和本来应该是基于 $m_{j-1}$ 来计算的:
$$ d_{j-1} = e^{x_1 - m_{j-1}} + e^{x_2 - m_{j-1}} + ... + e^{x_{j-1} - m_{j-1}} $$但是这跟上面前j-1项的贡献表示不同,所以我们要将 $d_{j-1}$ 转换为以 $m_j$ 为基准:
$$ \begin{aligned} e^{x_1 - m_j} + e^{x_2 - m_j} + ... + e^{x_{j-1} - m_j} &= e^{x_1 - m_{j-1} + m_{j-1} - m_j} + e^{x_2 - m_{j-1} + m_{j-1} - m_j} + ... + e^{x_{j-1} - m_{j-1} + m_{j-1} - m_j} \\\\ &=(e^{x_1 - m_{j-1}} + e^{x_2 - m_{j-1}} + ... + e^{x_{j-1} - m_{j-1}}) * e^{m_{j-1} - m_j} \\\\ &= d_{j-1} * e^{m_{j-1} - m_j} \end{aligned} $$所以:
$$ d_j = d_{j-1} * e^{m_{j-1} - m_j} + e^{x_j - m_j} $$FlashAttention-v1
背景动机
FlashAttention主要解决Transformer计算速度慢和存储占用高的问题。但与绝大多数Efficient Transformer把改进方法集中在降低模型的FLOPS(floating point operations per second)不同,FlashAttention将优化重点放在了降低存储访问开销(Memory Access Cost,MAC)上。
Transformer 复杂度可以理解为 $O(dN^2)$,这是因为 Self-Attention 的计算占据了 Transformer 的主要部分,而 Self-Attention 的复杂度为 $O(dN^2)$,主要为 $S = QK^T$ 和 $O = PV$ 的计算。
正因为Transformer的复杂度随序列长度的增长呈二次方增长,所以通常基于Transformer的大语言模型的上下文长度都不会特别长(如早期的大模型普遍在2k、4k左右)。

为了减少对HBM的读写,FlashAttention将参与计算的矩阵进行分块送进SRAM,来提高整体读写速度(减少了HBM读写)。
核心思想
前置知识:softmax计算的逐步更新(指数和逐步更新;最大值逐步更新)
分块累加见推导:From Online Softmax to FlashAttention
j=0,遍历 i:
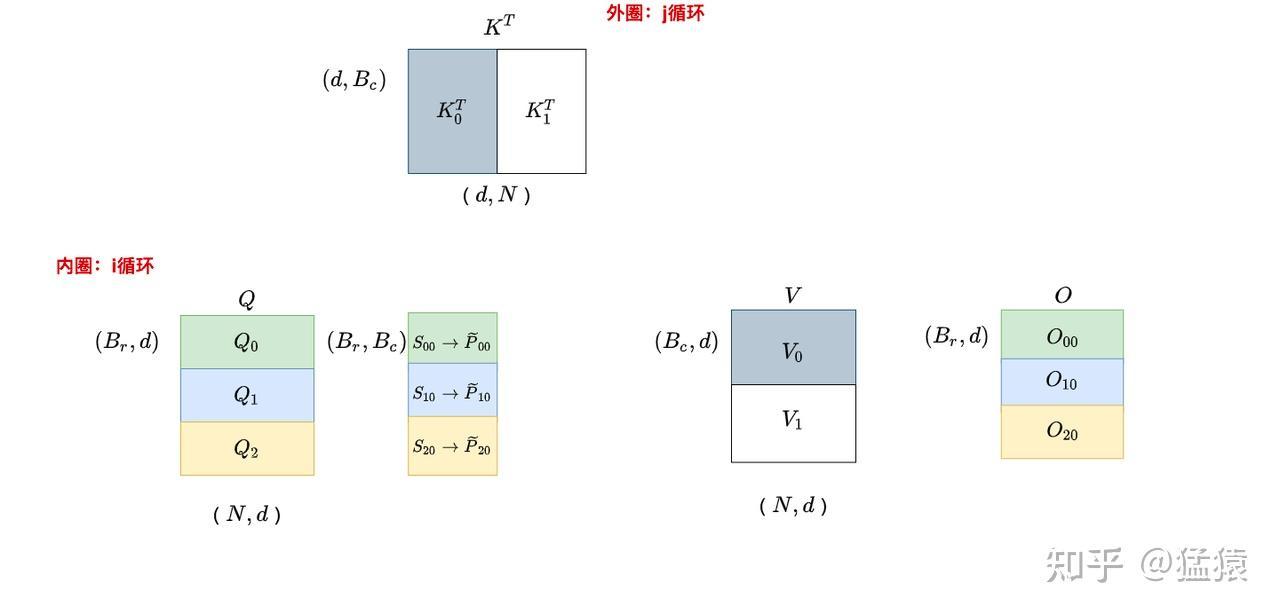
j=1,遍历i:
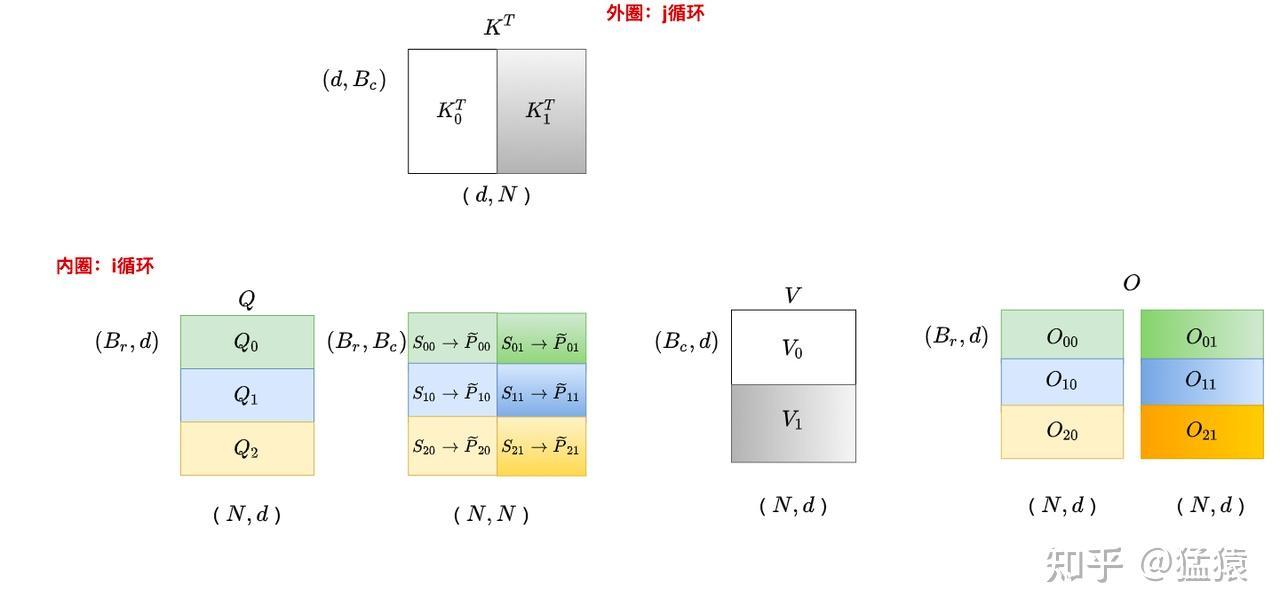
分块计算输出O:
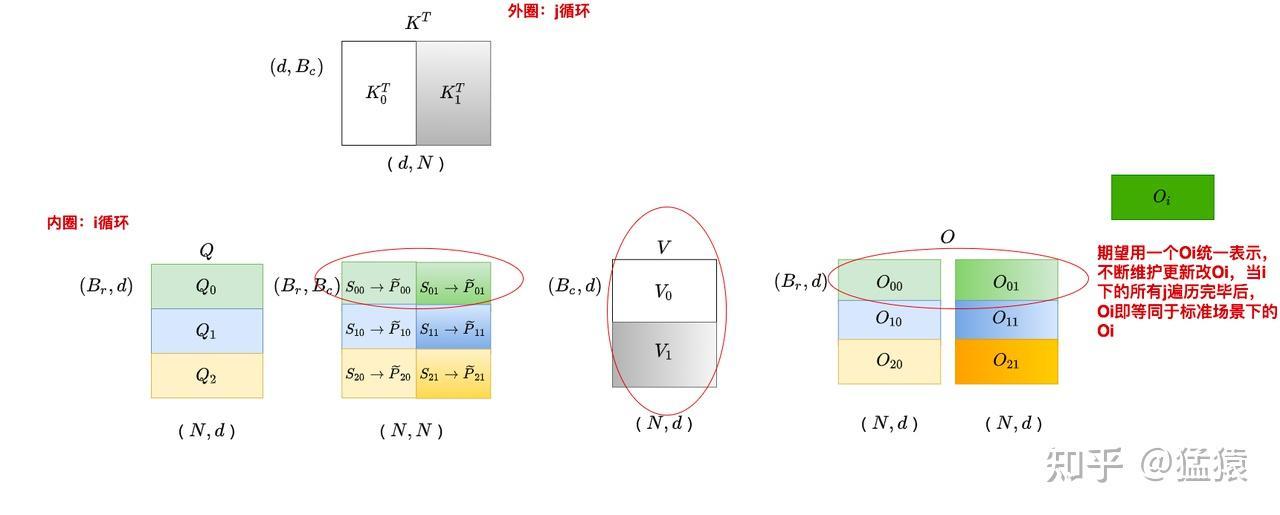
这里 $O$ 的更新可以看Ye推导公式,更新方式:
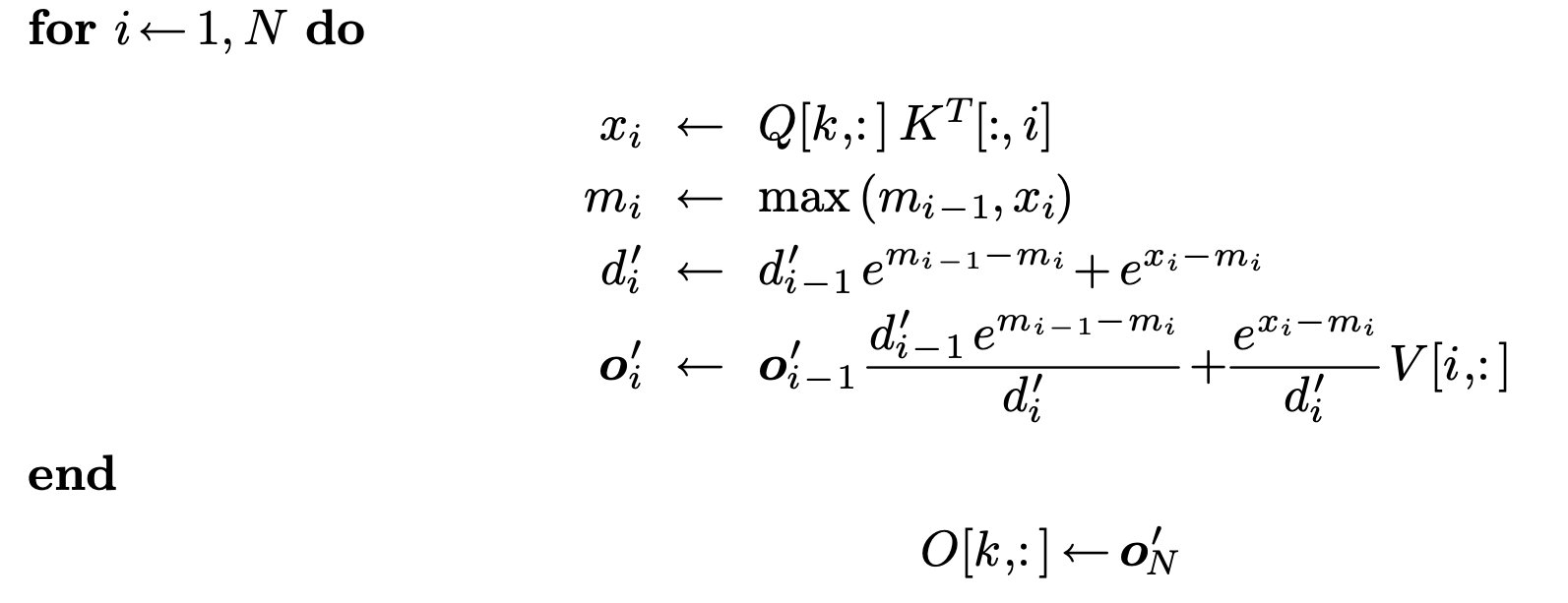
总体来看,不需要将 $S = QK^T$ 写入 HBM 再取回做 $Softmax$ 得到 $P$,然后再取回 $P$ 与 $V$ 做 $PV$ 得到结果。
内循环中,只需要计算分块后的 $S = QK^T$ 然后写入 SRAM,然后利用 $S$ 更新局部最大值 $m$ 和 局部指数和 $d$,然后与 $V$ 相乘后得到 $O$(必须乘以 $V$ 后这样才具有局部累加性)
FlashAttention-v2和v3
如果说FlashAttention-1 将一个大的注意力矩阵计算任务,分解成多个独立的“块”(tile)任务,由不同的线程块(thread block)并行处理。虽然这避免了高带宽内存(HBM)的读写,但每个线程块内部的计算仍然存在一些串行化和同步开销。
那么v2主要进一步优化了这种并行化。它让每个注意力头的计算任务,由一个线程束(warp) 而不是整个线程块来完成。一个线程束是 GPU 内部最小的执行单位(通常是 32 个线程)。这种设计使得每个线程束可以独立、高效地处理自己的任务,减少了不同线程块之间的同步和通信开销,从而提高了并发度。
并且采用了更优化的内存访问模式,更换q,kv的内外循环顺序等
而v3主要针对更长的上下文序列来进行一些特殊处理,
 支付宝
支付宝 微信
微信